How does Pauli exclusion principle cause the coupling term in Weizsäcker formula?
Consider the pairing term in Weizsäcker formula. here it is claimed that:
Due to the Pauli exclusion principle the nucleus would have a lower
energy if the number of protons with spin up were equal to the number
of protons with spin down.
I don't understand how Pauli exclusion principle should be the cause of this. This term comes from spin-spin interaction (or "coupling"), but I do not see the link with the fact that protons (or neutrons) with the same quantum numbers cannot occupy the same quantum state within a quantum system simultaneously
Consider the pairing term in Weizsäcker formula. here it is claimed that:
Due to the Pauli exclusion principle the nucleus would have a lower
energy if the number of protons with spin up were equal to the number
of protons with spin down.
I don't understand how Pauli exclusion principle should be the cause of this. This term comes from spin-spin interaction (or "coupling"), but I do not see the link with the fact that protons (or neutrons) with the same quantum numbers cannot occupy the same quantum state within a quantum system simultaneously
1 Answer
Here's my interpretation...
Recall that the strong nuclear force binds nucleons together.
Let's focus on protons.
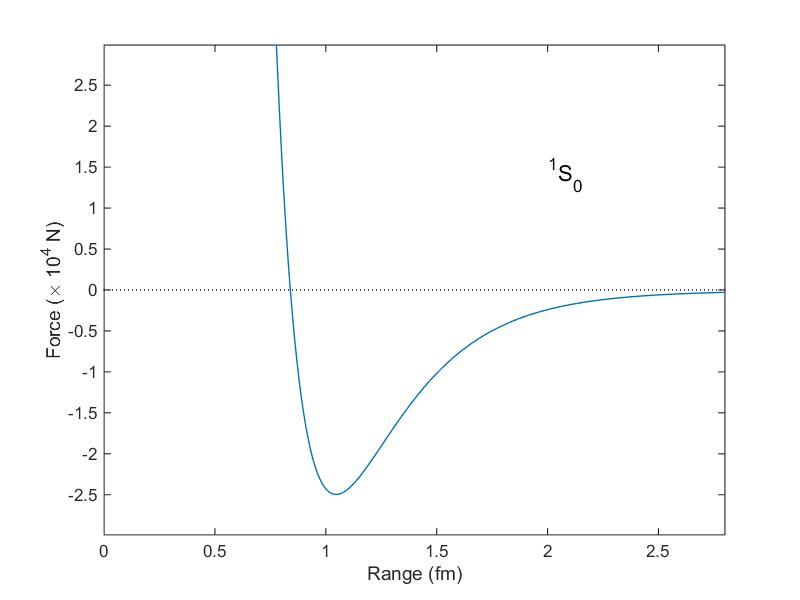
This force is stronger when the protons are aligned parallel, and weaker when they are aligned antiparallel (in fact, too weak in isolation to hold two protons together).
Two protons near enough can exchange mesons to create this force.
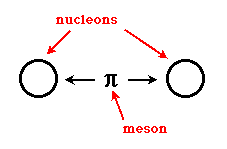
Due to the Pauli Exclusion Principle, since protons are fermions identical to each other, they cannot exist in the same quantum state except for (in this case, nuclear) spin.
This is most relevant for protons near enough to each other to interact (about 1 femtometer away), so if their spins are parallel, they're going to be somewhat attracted to each other (against the coulomb repulsive force) by this "strong" nuclear force.
If that were to happen and they come into the same quantum state... it is predicted that their wave functions "vanish", i.e. they don't physically exist (a fundamental nature of fermions to be antisymmetric under exchange).

On the other hand, if their spins are antiparallel, the strong nuclear force is generally too weak to hold them together (assuming neutrons are not nearby).
Thus, it becomes nicer to have neutrons available because nucleons of DIFFERENT types (protons vs. neutrons) CAN interact with the same spin.
As a result, we have this balance between:
- the interactions of different nucleons (proton with neutron) with the same spin, binding the nucleus together.
- the interactions of same nucleons (proton/proton, neutron/neutron), but with opposite spins to obey the Pauli Exclusion Principle.
And because of this, isotopes with an even number of protons and neutrons are able to have spin-up proton/neutron pairs, and spin-down proton/neutron pairs.
All of this minimizes the total energy of the nucleus by minimizing the total nuclear spin (which spreads out interaction energy evenly, maximizing system entropy), making such isotopes predominantly the most stable among all isotopes.

