Given: #(1−tan(x)) / (1+ tan(x))=1+sin(2x)#
Use the identity #tan(x) = sin(x)/cos(x)#
#(1−sin(x)/cos(x)) / (1+ sin(x)/cos(x))=1+sin(2x)#
Multiply the left side by 1 in the form of #cos(x)/cos(x)#
#cos(x)/cos(x)(1−sin(x)/cos(x)) / (1+ sin(x)/cos(x))=1+sin(2x)#
Follow rules for the multiplication of fractions:
#(cos(x)−cos(x)sin(x)/cos(x)) / (cos(x)+ cos(x)sin(x)/cos(x))=1+sin(2x)#
The cosines cancel:
#(cos(x)−sin(x)) / (cos(x)+ sin(x))=1+sin(2x)#
Use the identity #sin(2x) = 2sin(x)cos(x)#:
#(cos(x)−sin(x)) / (cos(x)+ sin(x))=1+2sin(x)cos(x)#
Multiply both sides by #(cos(x)+ sin(x))#
#cos(x)−sin(x) = (cos(x)+ sin(x))(1+2sin(x)cos(x))#
Perform the multiplication:
#cos(x)−sin(x) = cos(x) +2sin(x)cos^2(x)+ sin(x)+2sin^2(x)cos(x)#
Add #sin(x)-cos(x)# to both sides:
#2sin(x)cos^2(x)+ 2sin(x)+2sin^2(x)cos(x)= 0#
Divide both sides by 2:
#sin(x)cos^2(x)+ sin(x)+sin^2(x)cos(x)= 0#
Remove a common factor of #sin(x)#:
#sin(x)(cos^2(x)+sin(x)cos(x)+ 1)= 0#
The second factor has no real roots; I will prove this by graphing it:
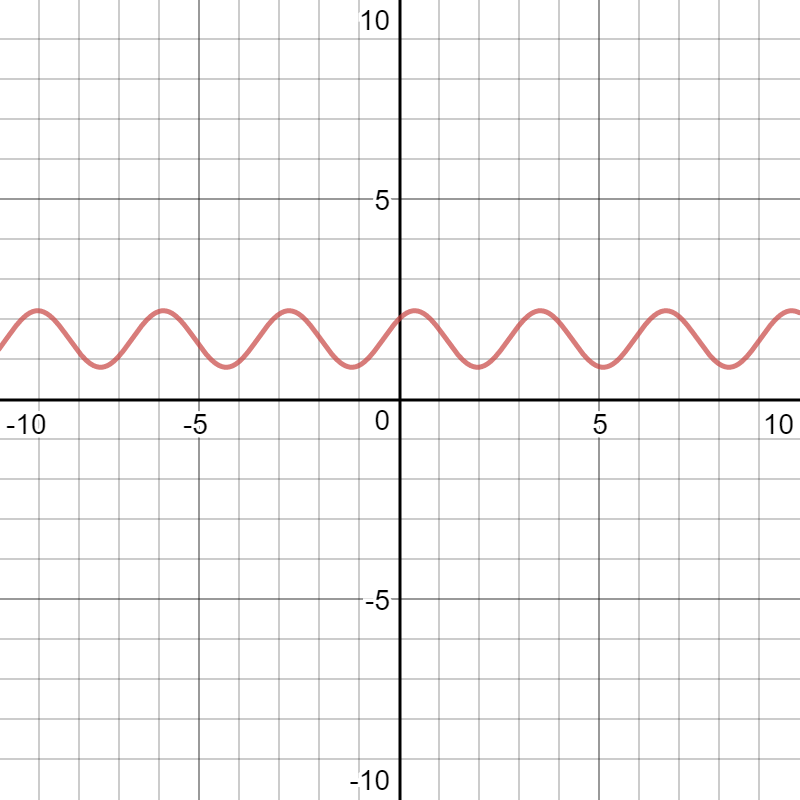
Please observe that the graph does not touch or cross the horizontal axis, therefore, the first factor is the only root.
#sin(x) = 0#
#x = sin^-1(0)#
#x = npi; n in ZZ#

