.
#int(t-2)/sqrt(27+6t-t^2)dt=int(t-2)/sqrt((-(t^2-6t-27)))dt=#
#int(t-2)/sqrt(-(t-9)(t+3))dt#
Let #u=t+3, :. du=dt#, and
#t=u-3, :. t-2=u-5, t-9=u-12, #
Let's substitute:
#=int(u-5)/sqrt(-(u-12)u)du=int(u-5)/sqrt(u(12-u))du=#
#int(u-5)/sqrt(12u-u^2)du#
Let's use trigonometric substitution:
We draw a right triangle and label an angle #theta# as shown below:
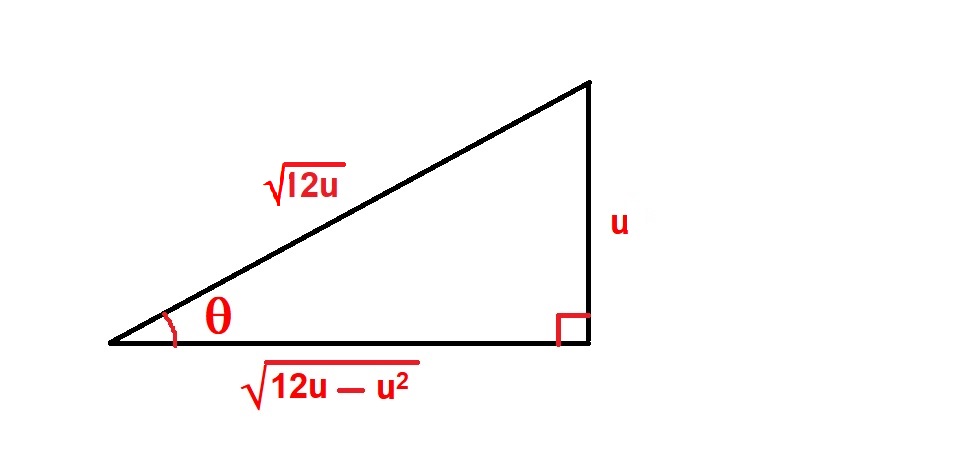
Now, we will right the basic trigonometric functions for the angle #theta#:
#sintheta=u/sqrt(12u)=sqrt(12u)/12#
#costheta=sqrt(12u-u^2)/sqrt(12u)#
#tantheta=u/sqrt(12u-u^2#
#sin^2theta=u^2/(12u)=u/12#
#2sinthetacosthetad theta=(du)/12#
#u=12sin^2theta#
#du=24sinthetacosthetad theta#
#sqrt(12u-u^2)=sqrt(12u)costheta=sqrt(12(12sin^2theta))costheta#
#sqrt(12u-u^2)=12sinthetacostheta#
Let's substitute:
#int(u-5)/sqrt(12u-u^2)du=int(12sin^2theta-5)/(12sinthetacostheta)(24sinthetacostheta)d theta=#
#2int(12sin^2theta-5)d theta=24intsin^2thetad theta-10intd theta=#
#24int(1-cos2theta)/2d theta-10theta=12intd theta-12intcos2thetad theta-10theta=#
#12theta-12I-10theta=2theta-12I#
#I=intcos2thetad theta#
Let #z=2theta, :. dz=2d theta, :. d theta=(dz)/2#
#I=1/2intcoszdz=1/2sinz=1/2sin2theta#
#2theta-12I=2theta-6sin2theta#
Using the double angle formula:
#sin2x=2sinxcosx#
#2theta-12I=2theta-12sinthetacostheta#
Let's substitute back for #u#:
#int(u-5)/sqrt(12u-u^2)du=2arcsin(sqrt(12u)/12)-12(sqrt(12u)/12)(sqrt(12u-u^2)/sqrt(12u))=#
#2arcsin(sqrt(12u)/12)-cancelcolor(red)(12)(cancelcolor(purple)(sqrt(12u)))/cancelcolor(red)(12)(sqrt(12u-u^2)/cancelcolor(purple)(sqrt(12u)))=#
#=2arcsin((sqrt(3u))/6)-sqrt(12u-u^2#
Now, we can substitute back for #t#:
#int(t-2)/sqrt(27+6t-t^2)dt=2arcsin(sqrt(3(t+3))/6)-sqrt(27+6t-t^2)+C#
This is one form of the solution. The result can be in many different forms depending on what you choose to be #u# and how you set up your triangle and what trigonometric functions you use.



