How is Gibbs free energy measured?
1 Answer
It's not measured. Actually, other MEASURABLE variables (volume and pressure) are measured in a certain way so that we can calculate
#color(blue)(DeltaG = int_(P_1)^(P_2) VdP)#
For the same-volume sample, change the pressure while keeping the temperature constant, and you can calculate
DISCLAIMER: This can be a difficult topic, so ask questions if you are confused.
If we take a look at this "thermodynamic square", we see the following terms:
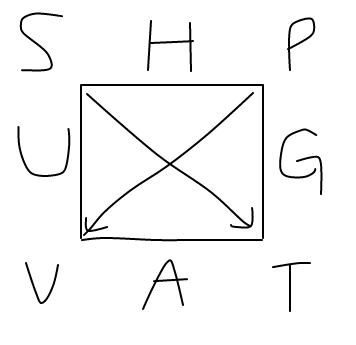
#S# for entropy, a natural variable, placed on a corner.#H# for enthalpy, a state function, placed on a side.#P# for pressure, a natural variable, placed on a corner.#U# for internal energy, a state function, placed on a side.#G# for Gibbs' Free Energy, a state function, placed on a side.#V# for volume, a natural variable, placed on a corner.#A# for Helmholtz Free Energy, a state function, placed on a side.#T# for temperature, a natural variable, placed on a corner.
From these we can derive the Maxwell Thermodynamics Relations.
Since I couldn't find this square anywhere, I actually had to draw it myself. So, let's derive a familiar relationship to show that this square works.
ENTHALPY VS. TEMPERATURE, ENTROPY, VOLUME, AND PRESSURE
Let's use this square to find a Maxwell relation for enthalpy.
Because one arrow points from the side of
The remaining terms placed right next to
So, we write:
#color(green)(dH = TdS + VdP)#
GIBBS FREE ENERGY VS. ENTROPY, TEMPERATURE, VOLUME, AND PRESSURE
Next, let's get a Maxwell relation for the Gibbs' Free Energy.
Since the arrow is pointing towards temperature AND coming from the side opposite to
Since
Therefore, we write:
#color(green)(dG = -SdT + VdP)#
I promise there's a point to this.
THE FAMILIAR THERMODYNAMICS EQUATION
So, let's compare
#dG = -SdT + stackrel(dH)(overbrace(VdP + TdS)) - TdS#
#= -(SdT + TdS) + dH#
Hm... Familiar. The first term is a result of a product rule.
#dG = dH - d(TS)#
Or, as a more familiar notation:
#color(green)(DeltaG = DeltaH - Delta(TS))#
Or, at a constant temperature, like we normally use this equation in this form:
#DeltaG = DeltaH cancel(- SDeltaT) + TDeltaS#
#\mathbf(DeltaG = DeltaH - TDeltaS) larr# FAMILIAR!
And you should know this equation! That means both equations we derived are correct.
HOW TO GET GIBBS' FREE ENERGY FROM MEASUREMENTS OF MEASURABLE VARIABLES
Now that we've established that, let's go back to the Gibbs' free energy Maxwell relation.
#dG = -SdT + VdP#
Let's say we wanted to focus on the
#color(green)(((delG)/(delP))_T = V)#
Next, at a constant temperature, let us find an expression to use volume and pressure (two MEASURABLE variables) to calculate the Gibbs' Free Energy:
#dG = VdP#
#color(blue)(DeltaG = int_(P_1)^(P_2) VdP)#
Therefore, if we know the volume of the sample, and we change the pressure while keeping the experiment temperature constant, we can calculate

