How is the fuction v(t)? And how to set the graph?
We have these information:
m(dv)/dt=g-R(v)
v(0)=0
We only know that R(v) is a increasing, continuous function, and R(0)=0 .
_ What are the proprieties of R(v) ?
What are the proprieties of v(t) ?
How is the graph of v(t) ?
Thank you.
We have these information:
We only know that
_ What are the proprieties of
What are the proprieties of
How is the graph of
Thank you.
1 Answer
See below.
Explanation:
This looks similar to falling of an object from height, maybe a paratrooper or a skydiver.
Since left hand side of the given expression has dimensions of force, and
with
We only know that
These two initial conditions and expression fits in the description well.
The weight of the object
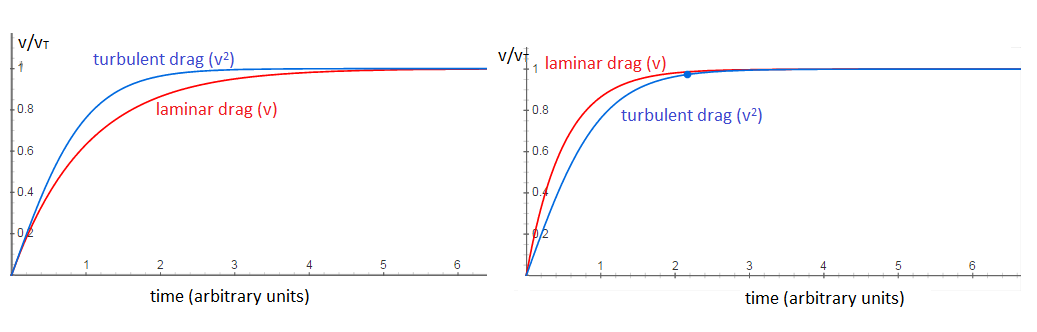
- At very low speeds for small objects, air resistance is approximately proportional to velocity and can be expressed in the form
For higher velocities and larger objects the frictional drag is approximately proportional to the square of the velocity and can be expressed as
where
2. When the body starts falling down its velocity keeps on increasing due to effect of gravity. With the increase in velocity the drag force increases as stated above, and it slows the object down.
There approaches a velocity when downwards force is equal to the drag force. This velocity
The expression reduces to
or Terminal velocity
3.  wikimedia.org/wikipedia
wikimedia.org/wikipedia
Any object falling through viscous medium accelerates quickly towards its terminal velocity, approaching gradually as the velocity gets nearer to the it.
