How is the radioactive decay of krypton-85 different from the radioactive decay of Americium-241?
1 Answer
Explanation:
The stability of a nucleus depends on the relative number of neutrons and protons — the neutron/proton ratio (
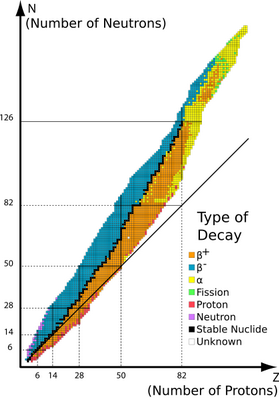
(from www.kentchemistry.com)
If
If
∴
The stable value is closer to 1.3, so
The atomic number increases by 1 unit, but the mass number stays the same.
There are now 37 protons and 48 neutrons.
The product is the stable, non-radioactive nuclide, rubidium-85.
Every nucleus with more than 82 protons is radioactive.

