Question

How is the velocity of an object represented?

Answer 1

Here's my interpretation.

Explanation:

I'm not sure I know exactly what the question asks, but here's some information:

An object's velocity is the rate of change of its position with time.

There are two main "types": average velocity and instantaneous velocity.

Average velocity is simpler to calculate, albeit slightly less useful, and is just the net change in the object's position (its displacement) divided by the time interval:

`vecv_"av" = (Deltavecr)/(Deltat)` (expressed in vector form)

or simply the magnitude,

`v_"av" = (Deltar)/(Deltat)`

On a position vs. time graph, the average velocity between two points at times `t_1` and `t_2` is the slope of the secant line of those two points:

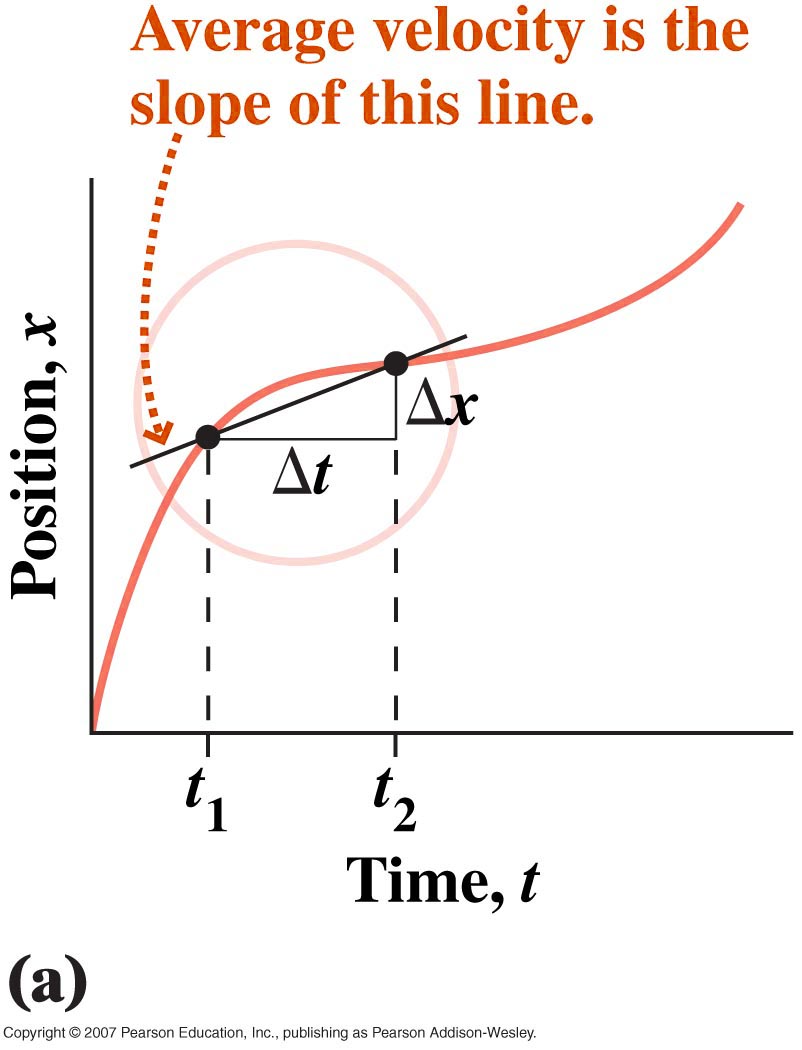
On the contrary, the instantaneous velocity is the velocity of the object at any given moment of time `t`.

The instantaneous velocity, denoted simply as `vecv` (magnitude `v`), is the limit of the average velocity as the time interval `Deltat` approaches `0`:

`v = lim_(Deltat rarr 0)v_"av" = lim_(Deltat rarr 0)(Deltar)/(Deltat)`

In calculus terms, the instantaneous velocity is the derivative of the object's position with respect to time:

`v = d/(dt)(Deltar)`

On a position-time graph, the instantaneous velocity of the object at any time `t` is the slope of the tangent line of the curve at that point:

In this image, we see that the velocity `vecv` at point `P` is the slope of the tangent line at `P`, and it can be found without the need of calculus by finding the average velocity at smaller and smaller time intervals.

(The three other lines represent the average velocity of the object between point `P` and points `Q`, `Q'`, and `Q''`. Each successive point is taken over a smaller time interval, and the smaller the time interval you take, the closer and closer you'll get to the actual velocity at that point. You can therefore find the instantaneous velocity of the object by finding the average velocity over increasingly shorter time intervals.)

If you're wondering how they're represented unit-wise, the velocity of an object is most often expressed in meters per second, `"m/s"`. Other units can obviously be derived via dimensional analysis, but most of the time it will be in `"m/s"`.