Question

How is the wave speed of a string the same as calculating the speed using kinematics?

I know the formula to find it, but I don't understand why it happens.

The formula is `v=sqrt(F_"T"/mu)`
=> where `v` is velocity in `m/s`, `F_"T"` is the tension in the string, and `mu` is the linear density - which is calculated by dividing the mass of the string with its length.

I want to know, how is the velocity calculated by this equation (^) is the same as velocity by kinematics, `v=(Deltad)/(Deltat)`.

How are the answers the same? (because they should be, right?)

Thank you for your time.

Answer 1

It can be like this

`v = sqrt(F_T/μ)`

`v = lamdaf" "`this equation is related to the earlier equation

`f = 1/"time required to cover a wavelength"`

`lamda = "wavelength"`

`therefore v = 1/"time required to cover a wavelength" * "wavelength"`

`v = (cancel"(wave)" "length")/("time required to cover" cancel("a wave")"length")`

`therefore v = "length"/"time"`

The speed of the wave is same as the velocity of the wave because standing waves only move in one direction.

To understand this we have to derive

`sqrt(F_T/u) = ω/k`

Let’s consider a string that has mass per unit length is μ. It is stretched by a tension T, which is much larger than the weight of the string and its equilibrium position is along the x axis. This diagram shows a short section of the string, stretched in the x direction, and the forces acting on it. Our analysis only applies for small deformations, for which the string is a linear medium, and we neglect the gravitational force on the string (which in any case is constant).

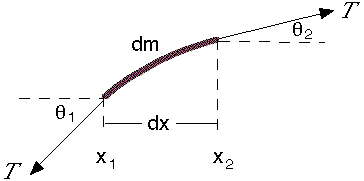
One consequence of this restriction to small deformations is that the angle θ between the string and the x direction is much smaller than 1, so `sin θ ≅ θ and cos θ ≅ 1`. (On our diagram, however, the deformation has been exaggerated for clarity.) It also follows that the length of the segment shown is dx.

Let's apply Newton's second law in the vertical y direction:

`F_y = ma_y`
The sum of forces in the y direction is
`F_y = T sin θ2 − T sin θ1.`

Using the small angle approximation, sin θ ≅ tan θ = ∂y/∂x. So we may write:

`F_y = T((∂y)/(∂x))_2 - T((∂y)/(∂x))_1`

So the total force depends on the difference in slope between the two ends: if the string were straight, no matter what its slope, the two forces would add up to zero. Now let's get quantitative. The mass per unit length is μ, so its mass `dm = μdx`. The acceleration in the y direction is the rate of change in the y velocity, so

`a_y = (∂v_y)/(∂t) = ( ∂y^2)/(∂t^2)`.

So we can write Newton’s second law in the y direction as

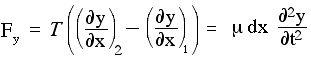
Rearranging this gives

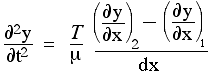
Now we have been using the subscript 1 to identify the position x, and 2 to identify the position `(x+dx)`. So the numerator in the last term on the right is difference between the (first) derivatives at these two points. When we divide it by `dx`, we get the rate of change of the first derivative with respect to `x`, which is, by definition, the second derivative, so we have derived the wave equation:

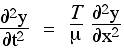
So the acceleration (on the left) is proportional to the tension T and inversely proportional to the mass per unit length μ. It is also proportional to `(∂y^2)/(∂x^2)`. So the a greater curvature in the string produces a greater acceleration and, as we have seen, a straight portion is not accelerated. This is the wave equation in one dimension. Now it is time to solve it.

A solution to the wave equation

This is a partial differential equation.One of the most popular techniques, however, is this: choose a likely function, test to see if it is a solution and, if necessary, modify it. So, let's use what we already know. We know that sine waves can propagate in a one dimensional medium like a string. And we know that any function `f(x − vt)` is a wave travelling at speed v. In the first chapter on travelling waves, we saw that an elegant version of the general expression for a sine wave travelling in the positive x direction is`y = A sin (kx − ωt + φ)`. A suitable choice of x or t axis allows us to set φ to zero, so let's look at the equation

`"y" = "A sin"(kx - ωt)`

to see whether and when this is a solution to the wave

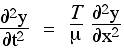
In taking the partial derivative with respect to t, we hold x constant and vice versa. So, remembering that the derivative of sine is cos and that the derivative of cos is minus sine, we can write the first two partial derivatives with respect to t and x like this:

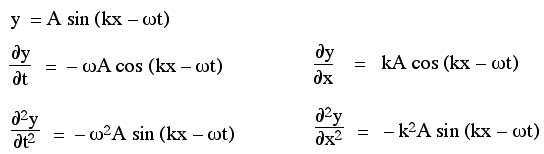
Wave speed in a stretched string

So we have seen that the second partial derivatives have the correct shape, which means we are on the right track. However, to be a solution to

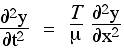
the partial derivatives

`ω/k = sqrt(F_T/μ)`

To understand where this equation comes from, consider a basic sine wave,`A cos (kx−ωt)`. After time t, the source has produced ωt/2π = ft oscillations`(omega = 2pif)`. After the same time, the initial wave front has propagated away from the source through space to the distance x to fit the same number of oscillations, kx = ωt.

Thus the propagation velocity v is `v = x/t= ω/k`. The wave propagates faster when higher frequency oscillations are distributed less densely in space.[2] Formally, `Φ = kx−ωt` is the phase. Since `ω = (−dΦ)/(dt)` and `k = (+dΦ)/(dx)`, the wave velocity is `v = (dx)/(dt) = ω/k`

And as

`k = 2pie" "e = 1/lamda`

Where e is spatial frequency

`k = (2pi)/lamda`

Therefore

`w/(2pi)/lamda = f/lamda`