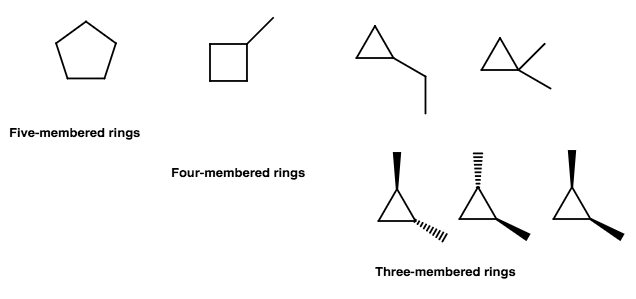
How many cyclic isomers does C5H10 have?

1 Answer
Truong-Son N.
Feb 12, 2018

I got #7# in total, including #R//S# stereoisomers.

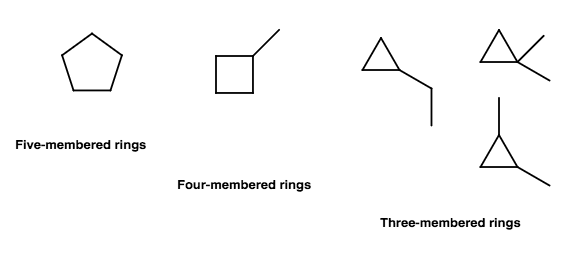
Since you just mention cyclic #"C"_5"H"_10#, we are not restricted to five-membered rings. I found:

In order, we have condensed formulas of:

  • #"C"_5"H"_10#
  • #"C"_3"H"_6"CH"-"CH"_3#
  • #"C"_2"H"_4"CH"-"CH"_2"CH"_3#
  • #"C"_2"H"_4"C"-("CH"_3)_2#
  • #"CH"_2("CHCH"_3)_2#

Or, if we decided to list the stereoisomers (#(R,R)#, #(S,S)#, #(R,S)#) of the three-membered rings, we would get two more. After all, stereoisomers are isomers!

Related questions
Impact of this question
27027 views around the world
You can reuse this answer
Creative Commons License