Question

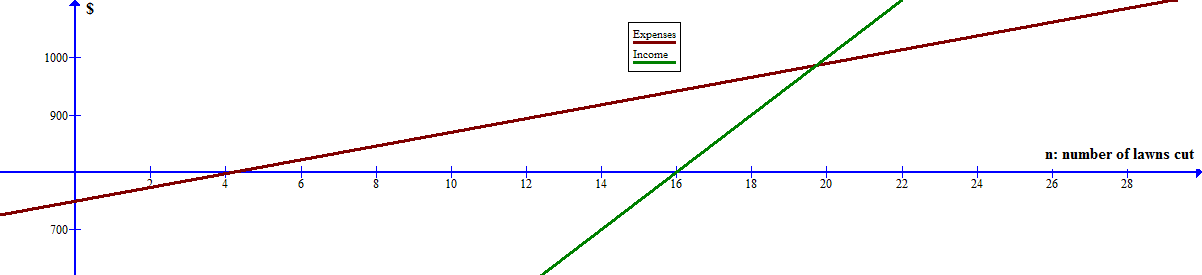
How many lawns does he have to landscape to break even?

Jamie wants to start a landscaping business. He buys $750 worth of equipment. Expenses for labor and gas are $12. He charges $50 per lawn. How many lawns does he have to landscape to break even? Write and solve a system of linear equations.

Answer 1

Expenses: `f(n)=750+12n`
Income: `color(white)("xx")g(n)=50n`
`color(white)("XXX")n`: number of lawns cut
`color(white)("XXX")`Both functions in dollar amounts.
Breakeven occurs while cutting the `20^"th"` lawn.

Explanation:

I assumed that the Expenses for labor and gas (`$12`) are per lawn.

The breakeven point occurs when Income `=` Expenses

`50n = 750+12n`

`rarr 38n=750`

`rarr n~~19.73...`

That is the breakeven point does not occur until after the `19^"th"` lawn.

Here are the Income and Expense functions with the intersection point being the breakeven point.