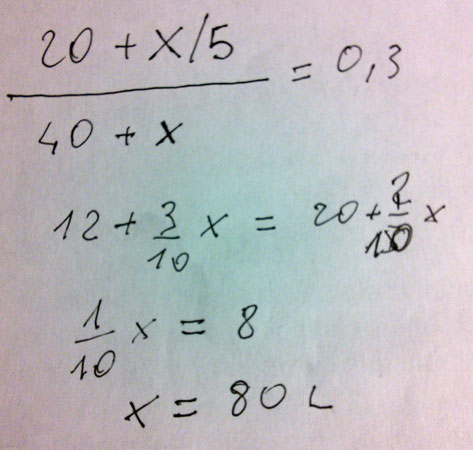How many liters of 20% alcohol solution should be added to 40 liters of a 50% alcohol solution to make a 30% solution?
1 Answer
OK. You must add 80 liters of 20% dilute solution to 40 liters of 50% concentrate solution get 120 liters of 30% solution at intermediate concentration.
After reflection I saw that I was unable to find a method by simple reflection. Because the final volume couldn't be determined in advance.
I wanted to avoid the use of mathematics, because I like qualitative or conceptual chemistry. However, at this point I was unable to find a shortcut or trick, so I used paper and pen, to get the result by ... trials and errors!!

I started adding 50 liters. Knowing that one fifth of 20% solution is alcohol and the other 4/5 are water, I obtained 90 liters of solution with 20+10 = 30 liters of alcohol and 20+40= 60 liters of water. So, 30 alcohol in 90 of water, that was a little more concentrated (it should be 30 alcohol by 100 total).
Then, I added just 10 liters more, getting 100 liters with 32 liters of alcohol in 68 liters of water, that is still more concentrated (it should be 30 by 70) .
So I made some more attempts, as 75 liters, obtaining 35 alcohol into 115 liters of solution, that yields 30,4%. Then, I was very close, and I tried 80 liters, that was the right one!
Sorry if I just used simple concepts of quantity and concentration, and not complicated maths.
Anyway, if you need a mathematical solution... here it is: