Question

How many molecules are in 48.90 grams of water?

Answer 1

`1.635 * 10^(24)" molecules"`

Explanation:

In order to figure out how many molecules of water are present in that `"48.90-g"` sample, you first need to determine how many moles of water you have there.

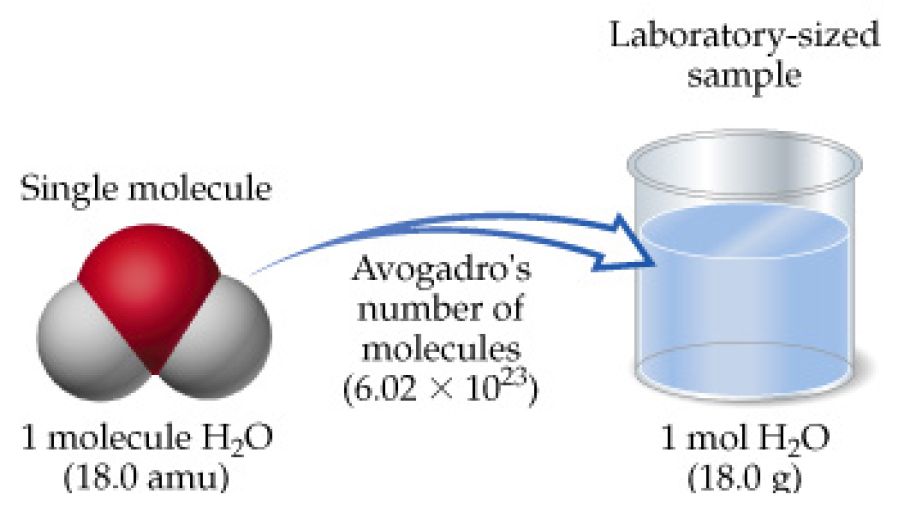
As you know, a mole is simply a very large collection of molecules. In order to have one mole of something, you need to have exactly `6.022 * 10^(23)` molecules of that something - this is known as Avogadro's number.

In order to get to moles, you must use water's molar mass. A substance's molar mass tells you the mass of one mole of molecules of said substance.

Water has a molar mass of `"18.015 g/mol"`. This means that one mole of water molecules has a mass of `"18.015 g"`.

So, to sum this up, `6.022 * 10^(23)` molecules of water will amount to `"1 mole"` of water, which in turn will have a mass of `"18.015 g"`.

So, use water's molar mass to find the number of moles present in that sample

`48.90 color(red)(cancel(color(black)("g"))) * ("1 mole H"_2"O")/(18.015color(red)(cancel(color(black)("g")))) = "2.7144 moles H"_2"O"`

Now use Avogadro's number to find the number of molecules of water

`2.7144 color(red)(cancel(color(black)("moles H"_2"O"))) * (6.022 * 10^(23)"molec.")/(1color(red)(cancel(color(black)("mole H"_2"O")))) = color(green)(1.635 * 10^(24)"molec.")`

The answer is rounded to four sig figs, the number of sig figs you have for the mass of water.