Question

How many nodes are on this standing wave? How many wavelengths are on this standing wave? What is the speed of the wave on the string? What is the wavelength of this standing wave? What is the frequency of this standing wave?

A 24.5 cm long string has a mass of 3.5 g and a tension of 8.6 kN. A standing wave of the 4th harmonic is created on the string.

Answer 1

(a) `5`
(b) `2lambda`
(c) `245.4ms^-1`, rounded to first decimal place
(d) `12.25cm`
(e) `approx 20Hz`

Explanation:

Given
A standing wave of the `4th` harmonic on a string.
Linear density of string `3.5/24.5 gcm^-1`

(a). Nodes on this standing wave
For a standing wave on the string, both ends must have have zero displacement, i.e., it is a node.

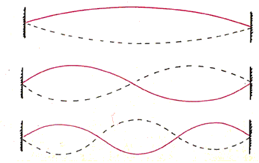
Above figure shows standing wave of `1st` harmonic to `3rd` harmonic.

General formulae for `nth` harmonic:
Number of nodes`=n+1`, Number of anti nodes`=n` and
Length of the string`=nlambda/2`
`:.` Number of nodes for `4th` hamonic`=4+1=5`

(b) No of wavelengths on standing wave.
Number of wavelengths on the string with `4th` harmonic `=4lambda/2 =2 lambda`, `2` wavelengths

(c). Speed of the wave on the string.
It can be obtained from the expression
Wave velocity `v=sqrt(T/mu)`, `T and mu` are tension and linear density of the string respectively. Inserting given values we obtain
`v=sqrt((8.6xx10^3)/(3.5/24.5))`
or `v=sqrt(8.6xx10^3xx24.5/3.5)`
or `v=sqrt60200`
or `v=245.4ms^-1`, rounded to first decimal place

(d). Wavelength of this standing wave.
It can be obtained from (b)
Length of string, `24.5=2lambda`
`implies lambda=24.5/2=12.25cm`

(e). frequency of this standing wave can be obtained from the expression
`v=fxxlambda`
Inserting various values
`245.4=fxx12.25`
`=> f=245.4/12.25approx 20Hz`