Question

How many positive numbers can be made from the digits 1, 2, 3, 4, 5, 6, 7, 8 and 9 so that they are smaller than 800? The digits can repeat.

Answer 1

`657` `"numbers"`.

Explanation:

These are numbers less than `800`, so they are at most `3` digit numbers.

So, make three slots:

_ _ _

The first slot can be filled with only `1,2,3,4,5,6 or 7` `(7` `"digits")` because the number is less than `800`. So, it can be filled in `7` ways.

Since repetition is allowed, the second and third slot can be filled in `9` ways each.

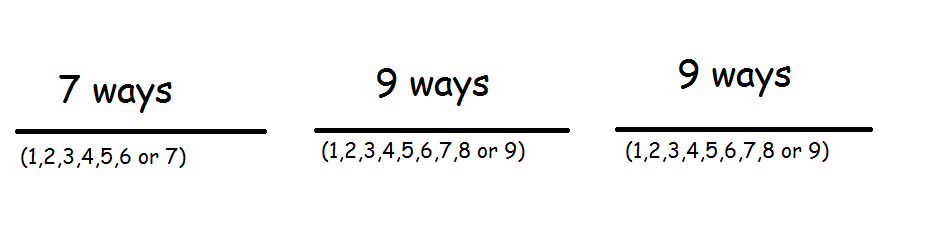
Now, multiply the number of ways:

`rarr7xx9xx9`

`color(green)(rArr567`

But wait, if we think about this, we notice that we can also form two-digit numbers and one-digit numbers less than `800.`

We can form `9` one digit numbers.

Now let's solve for the number of two-digit numbers. So put two slots:

_ _

We can write `9` digits in each of the slots:

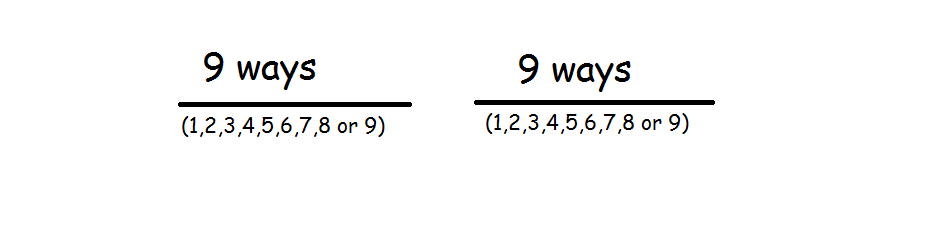
So there a total of `9xx9=81` ways.

Now, add all the numbers:

`rarr567+9+81`

`color(green)(rArr657`

Hope this helps!!! ☺•☻