Question

How many sides are in a regular polygon that has exterior angles of 40°?

Answer 1

A regular polygon with exterior angles of `40^o` would have 9 side and be a nonagon.

Explanation:

The exterior angles of any regular polygon must add up to `360^o`.

Since the angle measure given iin the questions s `40^o`, take `360^o/40^o` = 9. Meaning there are 9 exterior angles and therefore 9 sides to the polygon.

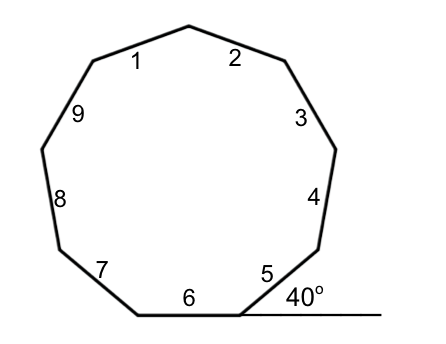
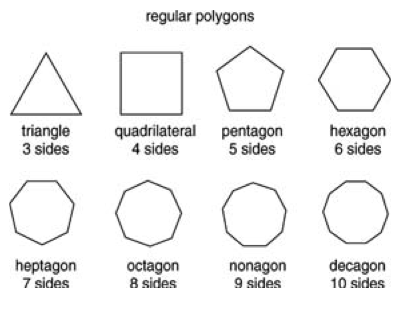
A regular polygon refers to a multi-sided convex figure where all sides are equal in length and all angles have equal degree measures.

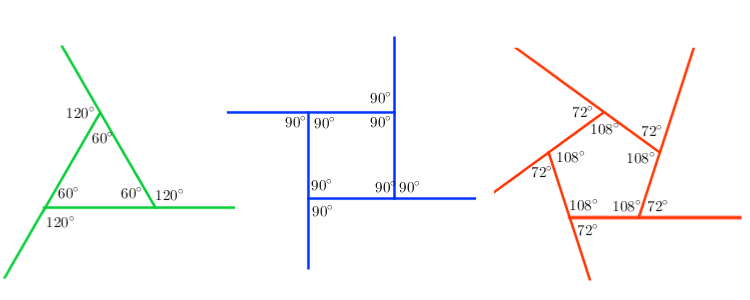
The regular triangle has 3 interior angles of `60^o` and 3 exterior angles of `120^o`. The exterior angle have a sum of `360^o` `=(3)120^o`

The square has 4 interior angles of `90^o` and 4 exterior angles of `90^o`. The exterior angle have a sum of `360^o` `=(4)90^o`.

The square has 5 interior angles of `108^o` and 5 exterior angles of `72^o`. The exterior angle have a sum of `360^o` `=(5)72^o`.

In order to find the value of the interior angle of a regular polygon the equation is `((n-2)180)/n` where n is the number of sides of the regular polygon.

Triangle `((3-2)180)/3 = 60^o`
Square `((4-2)180)/4 = 90^o`
Pentagon `((5-2)180)/5 = 72^o`

Finally

The interior and exterior angles of a regular polygon form a linear pair and therefore are supplementary and must add up to `180^o`.