Question

How many values of c satisfy the conclusion of the Mean Value Theorem for f(x) = x^3 + 1 on the interval [-1,1]?

Answer 1

There are two values of `c` that work.

Explanation:

The derivative of `f` is `f'(x)=3x^2`. The slope of the secant line is `(f(1)-f(-1))/(1-(-1))=(2-0)/2=1`. Setting `f'(x)=1` and solving for `x` results in `x=\pm 1/sqrt{3}`. These are the two "`c`" values, and they are in the interval `[-1,1]`.

Here's a picture for the given situation:

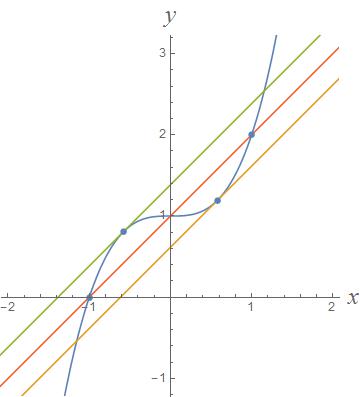
The red line is the secant line between `(-1,f(-1))=(-1,0)` and `(1,f(1))=(1,2)`. The green line is the tangent line to `f` at `(-1/sqrt(3),f(-1/sqrt(3)))\approx (-0.577,0.808)` and the gold line is the tangent line to `f` at `(1/sqrt(3),f(1/sqrt(3)))\approx (0.577,1.192)`. All these lines are parallel with a slope of 1.