How many wavelengths are on this spring? What is the wavelength of this standing wave? What is the speed of the wave on the spring? What is the tension on the spring? What is the mass of the spring?
A mechanical oscillator has a frequency of 130 Hz and creates a standing wave of the 9th harmonic when attached to a 62.2 cm long spring that has a linear density of 8.5 g/cm.
A mechanical oscillator has a frequency of 130 Hz and creates a standing wave of the 9th harmonic when attached to a 62.2 cm long spring that has a linear density of 8.5 g/cm.
2 Answers
- There are 4.5 wavelengths.
# λ = 0.14m# #v = 18 m.s^(-1)#
Explanation:
For standing waves on springs / strings there are always nodes at each end. And the number of antinodes is equal to the harmonic that we are considering – in this case the ninth harmonic so there are 9 antinodes.
1. How many wavelengths?
At the ninth harmonic there are 9 antinodes and 10 nodes. The number of antinodes corresponds with the number of halves of wavelengths. Or put another way there are 9 node-to-node sections on the wave and each section has a length of half a wavelength.
So there are 9 × 0.5 = 4.5 wavelengths.
2. What is the wavelength?
We are told that the length of the spring is:
In part 1 we found that along that total length are 4.5 wavelengths. So we can equate the two and solve for the wavelength:
3. Speed of the wave?
Use the wave speed equation, we are told the frequency of the generator in the question:
Not sure about the final two parts, perhaps someone can collaborate and finish off? If not I will try to get back to this ASAP.
(a)
Explanation:
Given
A mechanical oscillator having frequency of
Creates a standing wave of the
Linear density of spring
(a). No of wavelengths are on this spring.
As the oscillator is oscillating with its fundamental frequency, (one complete wavelength), as such both end have zero displacement. Since oscillator create s a standing wave in the spring, both ends of the spring also have zero displacement, i.e., it is a node.
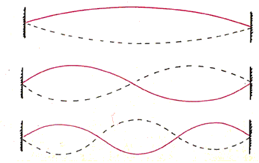
Above figure shows standing wave of
General formulae for
Number of nodes
Length of the spring
(b). Wavelength of this standing wave.
Length of the spring
(c). Speed of the wave on the spring.
It can be obtained from the expression
(d) Tension on the spring
There is no direct relationship for calculating tension in the spring.
However, we can use the formula for tension in the string.
Where wave velocity
(e) Mass of the spring.
Mass of the spring

