Question

How much higher is the ladder now?

Answer 1

`" "`
The ladder moves `color(red)("8 feet"` higher.

Explanation:

`" "`
`color(green)("Step 1"`

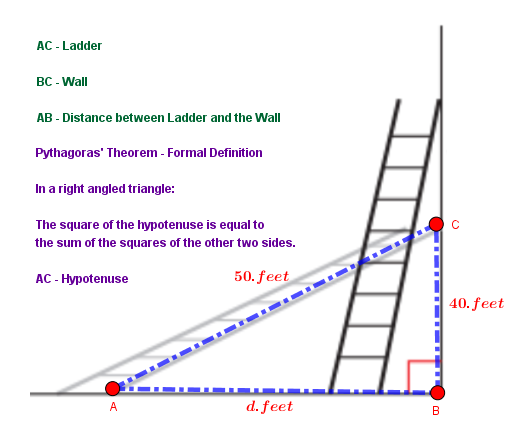
Observe the sketch below:

`color(green)("Step 2"`

Triangle `color(blue)(ABC` is a right-triangle.

`color(red)(AC` is the Hypotenuse, as `color(red)(AC` is the side opposite to the right-angle at `color(red)(B`.

`color(blue)("AC = 50 feet"`.

Let `color(blue)("AB = d feet"`.

`color(blue)("BC = 40 feet"`.

Using the Pythagoras' Theorem

`(AC)^2 = (AB)^2+(BC)^2`

`50^2=d^2+40^2`

`2500=d^2+1600`

`d^2+1600=2500`

Subtract `color(red)(1600` from both sides of the equation.

`d^2+1600-color(red)(1600)=2500-color(red)(1600`

`d^2+cancel 1600 - color(red)(cancel 1600)=900`

`d^2=900`

Take Square Root on both sides

`sqrt(d^2) = sqrt(900`

`color(blue)(d = 30`

`color(red)( :. " AB = 30 feet"`

`color(green)("Step 3"`

We know that the ladder (AC) moves up `color(red)"x feet"` from its initial position.

Observe the sketch given below:

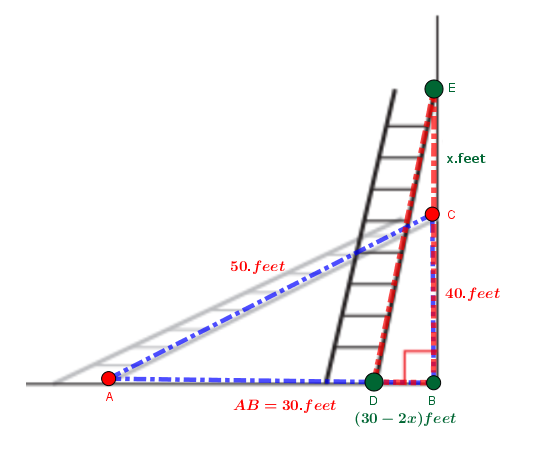
Focus on the right-triangle `color(red)(DBE`.

`"CE = x feet"`.

`"DB = ( 30 - 2x ) feet"`, as `color(blue)("AB = 30 feet"` from the previous step.

`BE =BC+CE= (40+x)` feet.

`color(green)("Step 4"`

Using Pythagoras' Theorem

`color(blue)((DE)^2=(BD)^2+(BE)^2`

`50^2=(30-2x)^2+(40+x)^2`

Note: `color(green)((a+-b)^2=a^2 +- 2ab+b^2)`

`50^2={30^2-120x+(2x)^2} + {40^2+80x+x^2}`

`2500={900-120x+4x^2}+{1600+80x+x^2}`

`2500=4x^2+x^2-120x+80x+1600+900`

`2500=5x^2-40x+2500`

Subtract `color(red)(2500` from both sides

`5x^2-40x+cancel 2500-color(red)(cancel 2500)=2500-color(red)(2500`

`5x^2-40x=0`

`5x(x-8)=0` ( 5x is the common factor)

`(5x)=0 or (x-8)=0`

If `5x=0, x=0` ( Ignore - NOT suitable )

`x-8=0`

Add `color(red)(8` to both sides.

`x-cancel 8+color(red)(cancel 8)=0+color(red)(8`

`x=8`

Hence, `CE=8`

Hence, the ladder moves `color(red)("8 feet"` higher.

Answer 2

`x=8`

Explanation:

The ladder makes a right triangle with the wall. `30^2 + 40^2=50^2 quad` is a variation on everyone's favorite Pythagorean Triple. So the initial position of the base is 30 feet from the wall.

After the top moves up `x` it's at `40+x.` The base is `30-2x.`

`(30 - 2x)^2 + (40 + x)^2 = 50^2`

`30^2 - 120 x + 4x^2 + 40^2 + 80 x + x^2 = 50^2`

`5x^2 - 40 x = 0`

`5x(x - 8) = 0`

We can rule out `x=0` so

`x=8`

Check:

`(30-2(8))^2 = 14^2 = 196`

`(40+8)^2=48^2=2304`

`196+2304=2500=50^2 quad sqrt`