How does the bond energy for the formation of #"NaCl"(s)# take place? Please explain in steps comprehensively but concisely. Thank you in advance.
1 Answer
Do you mean the energy involved in the process to form
I get:
#DeltaH_"lattice" -= -|DeltaH_"lattice"|#
#= -[DeltaH_(f,"NaCl"(s))^@ + DeltaH_("sub","Na") + "IE"_(1,"Na"(g)) + 1/2DeltaH_("bond","Cl"_2(g)) - "EA"_(1,"Cl"(g))]# ,
where all the numbers you plug in to the righthand side are positive.
Formation reactions generate
(You should check your textbook to see whether it is defined as
Elemental state simply means the natural state you find them at typical life conditions.
- Sodium is a metal at room temperature and pressure.
- Chlorine is a diatomic gas at room temperature and pressure.
So, the balanced formation reaction is:
#"Na"(s) + 1/2"Cl"_2(g) -> "NaCl"(s)#
Note that there exists a negatively-signed lattice energy for the following reaction:
#"Na"^(+)(g) + "Cl"^(-)(g) -> "NaCl"(s)#
since forming the lattice stabilizes the components (we went from two gases to one solid, creating order), decreasing their overall energy.
These share the same product, so let's say we wanted to form the following cycle:
#"Na"(s) + 1/2"Cl"_2(g) -> [...] -> "Na"^(+)(g) + "Cl"^(-)(g) -> "NaCl"(s)#
This would be what we call the Born-Haber thermodynamic cycle. This is allowed since enthalpy is a state function, which does not depend on the path.
As it turns out, the lattice energy is difficult to acquire in real life, so it is often indirectly obtained from calculations not unlike the ones we're doing.
Our goal is to fill in the missing steps by transforming each element one step at a time (phases, charges, and chemical bonds):
#"Na"(s) stackrel("Sublimation")overbrace(->) "Na"(g) stackrel("1st Ionization")overbrace(->) "Na"^(+)(g)#
#1/2"Cl"_2(g) stackrel(1/2xx"Bond-Breaking")overbrace(->) "Cl"(g) stackrel("1st Electron Affinity")overbrace(->) "Cl"^(-)(g)#
For simplicity in our Born-Haber cycle, let up use positive numbers and down use negative numbers.
Then, the following reactions would be involved to transform each reactant for the formation of
#"NaCl"(s) -> "Na"(s) + 1/2"Cl"_2(g)# ,#-DeltaH_(f,"NaCl"(s))^@ = "411 kJ"#
#"Na"(s) -> "Na"(g)# ,#DeltaH_("sub","Na") = "107 kJ"#
#"Na"(g) -> "Na"^(+)(g) + e^(-)# ,#"IE"_(1,"Na"(g)) = "502 kJ"#
#1/2"Cl"_2(g) -> "Cl"(g)# ,#1/2DeltaH_("bond","Cl"_2(g)) = 1/2xx"242 kJ"#
#"Cl"(g) + e^(-) -> "Cl"^(-)(g)# ,#"EA"_(1,"Cl"(g)) = -"355 kJ"#
#"Na"^(+)(g) + "Cl"^(-)(g) -> "NaCl"(s)# ,#DeltaH_"lattice" = ???#
#"-----------------------------------------------------------------------------"#
#"These cancel out completely upon adding, proving"#
#"we have a complete cycle."#
Put that together by adding all the given energies, and you'll have the following diagram:
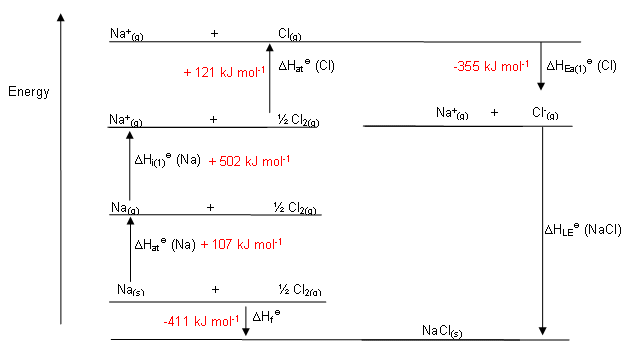
Take the
#0 = DeltaH_"cycle" = DeltaH_(f,"NaCl"(s))^@ + DeltaH_("sub","Na") + "IE"_(1,"Na"(g)) + 1/2DeltaH_("bond","Cl"_2(g)) - "EA"_(1,"Cl"(g)) - DeltaH_"lattice"#
Solving for
#color(blue)(DeltaH_"lattice" -= -|DeltaH_"lattice"|)#
#= color(blue)(-[DeltaH_(f,"NaCl"(s))^@ + DeltaH_("sub","Na") + "IE"_(1,"Na"(g)) + 1/2DeltaH_("bond","Cl"_2(g)) - "EA"_(1,"Cl"(g))])#
where all the numbers you plug in are positive. For example, we'd get:
#color(blue)(DeltaH_("lattice","NaCl"(s)))#
#= -[411 + 107 + 502 + 1/2(242) - 355] "kJ"#
#= color(blue)(-"786 kJ")#

