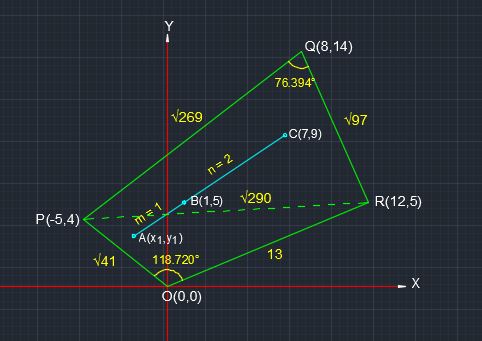
a) i)
Use the distance formula: #d = sqrt((x_2-x_1)^2 + (y_2-y_1)^2)# to find the length #OP,PQ,QR,PR, and OR#,
#OP=sqrt((-5-0)^2+(4-0)^2)=sqrt(25+16)=sqrt41# m
#PQ=sqrt((8+5)^2+(14-4)^2)=sqrt(13^2+10^2)=sqrt269# m
similarly, #QR=sqrt97# m, #PR=sqrt290# m, and
#OR=sqrt169=13# m
Use the law of cosines to find #anglePQR#
#PR^2=PQ^2+QR^2-2*PQ*QR*cosanglePQR#,
#=> cosanglePQR=(PQ^2+QR^2-PR^2)/(2*PQ*QR)#,
#=> anglePQR=cos^-1((269+97-290)/(2*sqrt269*sqrt97))=76.394^@#
similarly,
#anglePOR=cos^-1((OP^2+OR^2-PR^2)/(2*OP*OR))#
#=cos^-1((41+169-290)/(2*sqrt41*13))=118.720^@#
area of #DeltaPQR=A_1=1/2*PQ*QR*sinanglePQR#
#=1/2*sqrt269*sqrt97*sin76.394=78.50 " m"^2#
area of #DeltaPOR=A_2=1/2*OP*OR*sinanglePOR#
#=1/2*sqrt41*13*sin118.720=36.5 " m"^2#
#=># area of #OPQR=A_1+A_2=78.5+36.5=115.00 " m"^2#
a) ii)
Section formula :
If a point #B(x,y)# divides a line segment joining #A(x_1,y_1)and C(x_2,y_2)# in the ratio of #m:n#, i.e., #(AB:BC=m:n)#,
then #B(x,y)= ((mx_2+nx_1)/(m+n), (my_2+ny_1)/(m+n))#
Given that #B=(1,5) and C=(7,9)# and #C# is 2 times from #B#, and 3 times from #A#,
#=> AB:BC=1:2, => m:n=1:2#
let coordinates of #A=(x_1,y_1)#,
#=> B(1,5)=((1xx7+2x_1)/(1+2),(1xx9+2y_1)/(1+2))#
#=> (x_1,y_1)=(-2,3)#
Hence #A(x_1,y_1)=A(-2,3)#


