Question

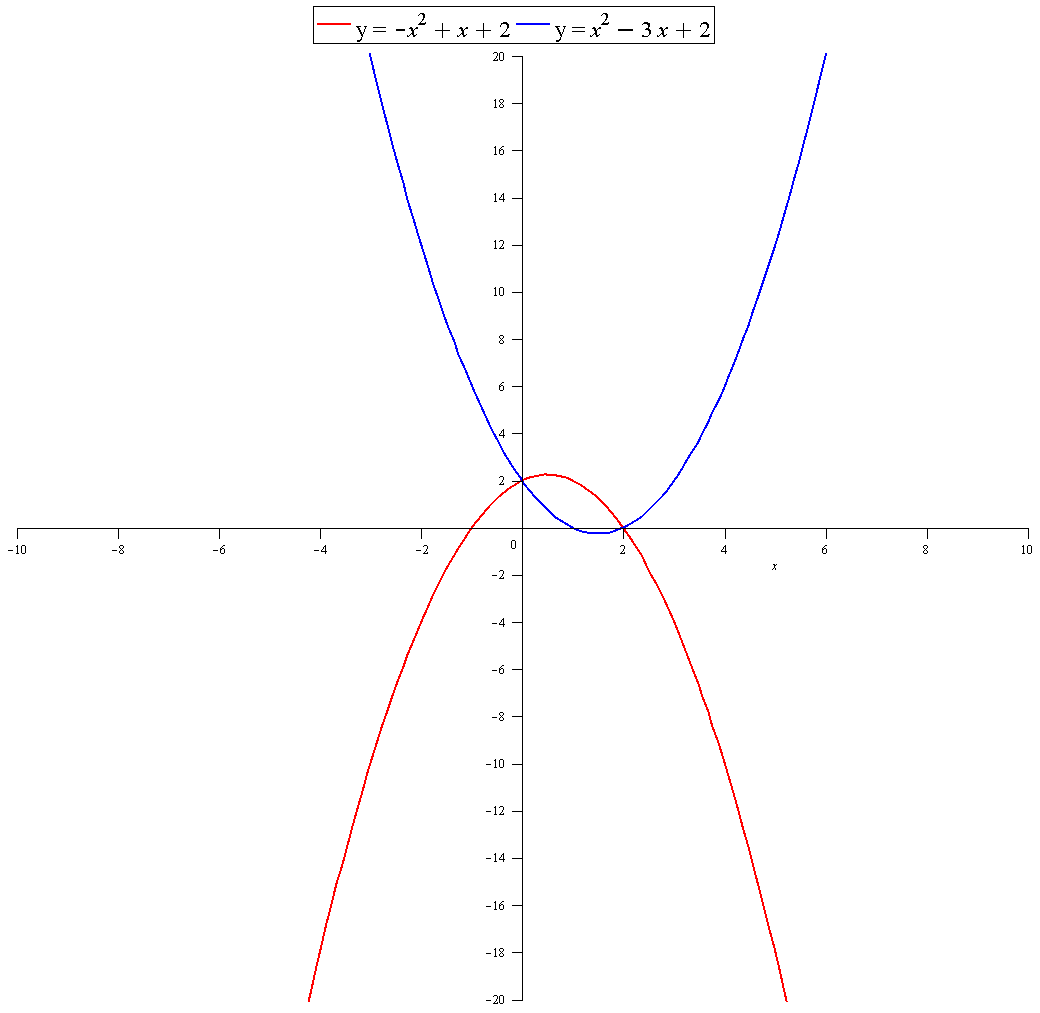
How to calculate area between `y_1=x^2-3x+2` and `y_2=-x^2+x+2`?

I tried to solve the disequation `y_1>=y_2` and that means `x < 0` OR `x\ge2`, so I've calculated `int_0^2 y_1-y_2= -8/3`

Answer 1

13/3

Explanation:

First we must find where they intersect by equating them to each other:

`x^2-3x+2=-x^2+x+2`

`=>2x^2-4x=0`

`=>x^2-2x=0`

`=>x(x-2)=0`

`=>x = 2 or 0`

Now to find the area, first we must Add the blue and green areas, and subtract the red area

{Red line = `x^2-3x+2`}
{Blue line = `-x^2+x+2`}

Blue area:
`int_0^2(-x^2+x+2)dx`

`=-x^3/3+x^2/2+2x|` `0->2`

`=-(2)^3/3+(2)^2/2+2(2)`

`=-8/3+2+4=10/3`

Green Area:

To find exactly where `x^2-3x+2` intersects the X-Axis, we must solve for x in-
`x^2-3x+2=0`

`=>x=1 or 2`

To find the area-
`int_1^2(x^2-3x+2)dx`

`=x^3/3-3/2x^2+2x|` `1->2`

`=(2)^3/3-3/2(2)^2+2(2)-((1)^3/3-3/2(1)^2+2(1))`

`=8/3-12/3+4-1/3+3/2-2=11/6`

Red Area:

Simple integral-

`int_0^1(x^2-3x+2)dx`

`=x^3/3-3/2x^2+2x|` `0->1`

`=(1)^3/3-3/2(1)^2+2(1)`

`1/3-3/2+2=5/6`

Now the total area = Blue + Green - Red = `10/3+11/6-(5/6)=13/3`

Answer 2

`8/3` cubic units.

Your answer was correct except for the negative sign.

Explanation:

The easiest way to solve this is to first note from the graph, that if we translate both curves in the positive `y` direction by a given amount, we can eliminate the problem of the areas being both above and below the `x` axis. Translating vertically will not affect the points of intersection, nor the boundary values in relation to the x axis.

So if we translate by say 2 units we the have:

`y_1=x^2-3x+4` and `y_2=-x^2+x+4`

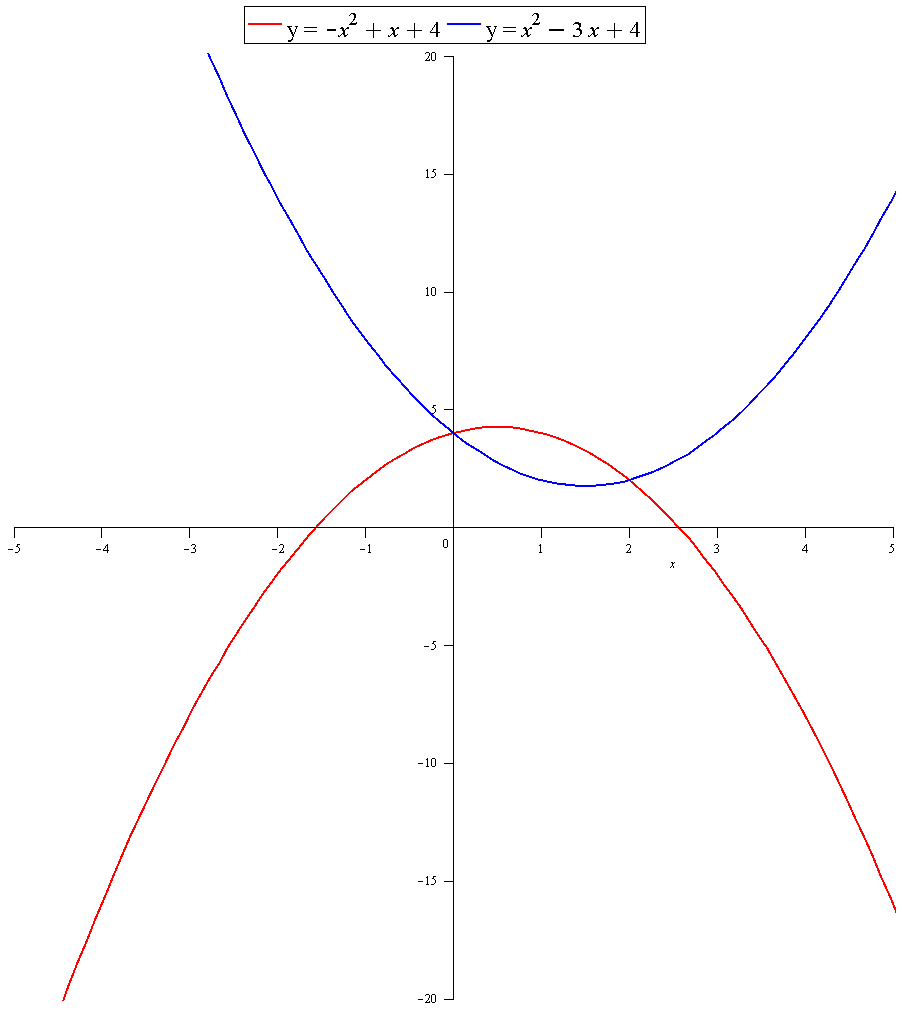
Intersection of `y_1 and y_2`

`x^2-3x+4=-x^2+x+4`

#2x^2-4x=0

`x(x-2)=0=>x=0 and x=2`

We can see from the graph that if we find:

`int_(0)^(2)(-x^2+x+4) dx`

And subtract:

`int_(0)^(2)(x^2-3x+4) dx` , this will be the required area.

i.e.

`int_(0)^(2)(-2x^2+4x) dx`

`int_(0)^(2)(-2x^2+4x) dx=[-2/3x^3+2x^2]_(0)^(2)`

`Area=[-2/3x^3+2x^2]^(2)-[-2/3x^3+2x^2]_(0)`

Plugging in bounds:

`Area=[-2/3(2)^3+2(2)^2]^(2)-[-2/3(0)^3+2(0)^2]_(0)`

`Area=[-2/3(2)^3+2(2)^2]=[-16/3+8]=8/3` cubic units.