How to calculate the exponents in the differential rate law?
GIVEN:
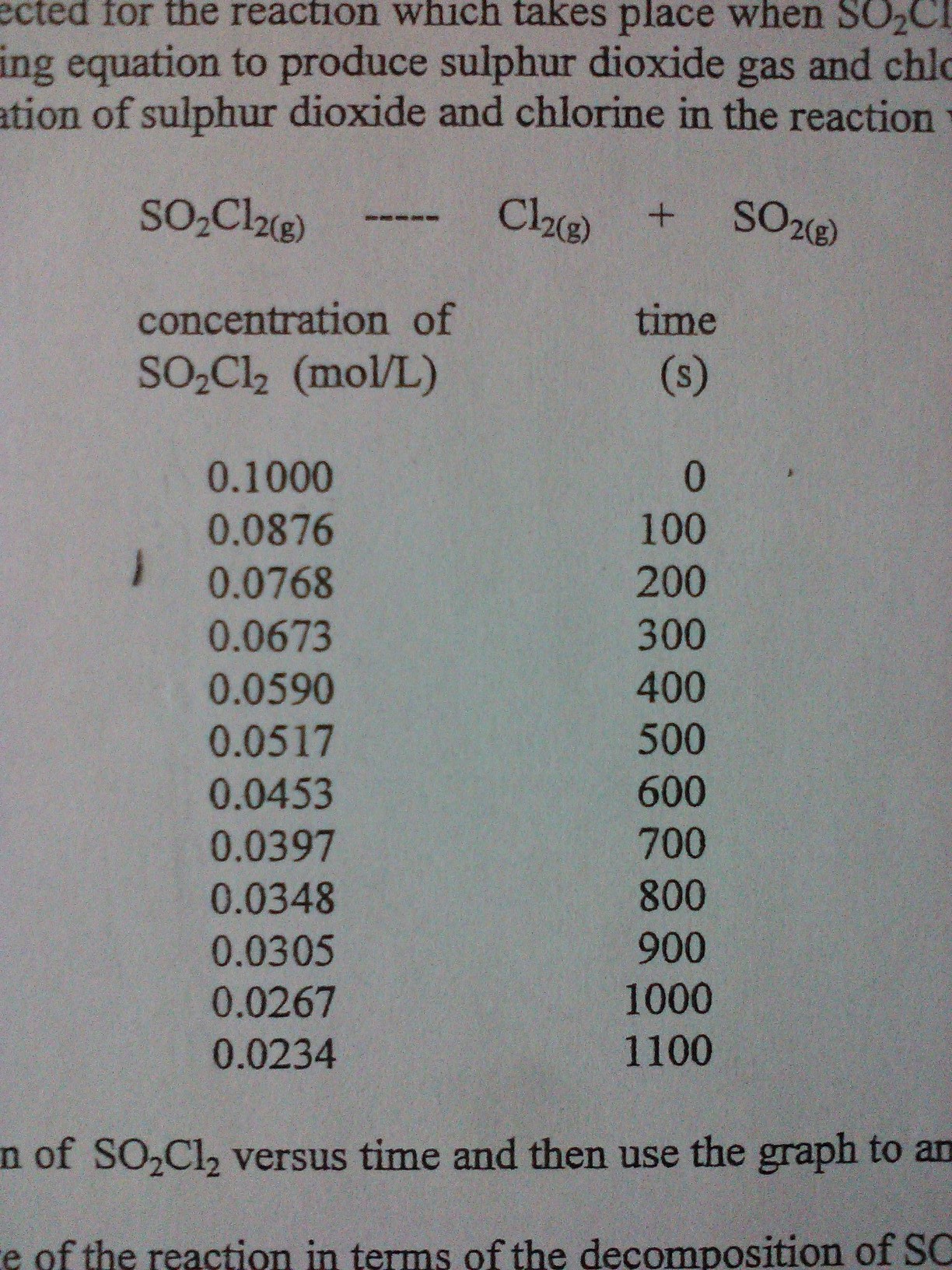
GIVEN:

2 Answers
You use the formulas from the integrated rate laws.
Explanation:
Shen you have a list of concentrations as a function of time, you want to plot something that gives a straight line.
The equation for a straight line is:
#color(blue)(bar(ul(|color(white)(a/a) y = mx + b color(white)(a/a)|)))" "#
We can write the integrated rate laws for zero-, first, and second-order reactions all as straight-line functions.
Thus,
- For a 0-order reaction, a plot of
#c# vs#t# should give a straight line with slope#"-"k# - For a 1st-order reaction, a plot of
#ln(c)# vs#t# should give a straight line with
slope#"-"k# - For a 2nd-order reaction, a plot of
#1/c# vs#t# should give a straight line with slope#k#
So, we plot each of these functions and see which gives the best straight line.
I used Excel to convert your data into the following table.
Then I plotted each of the three functions.
Zero-Order Plot
The graph appears to be a curve.
First-Order Plot
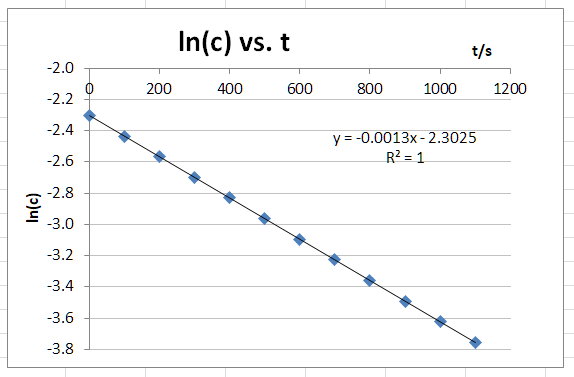
The graph appears to be a straight line.
Second-Order Plot
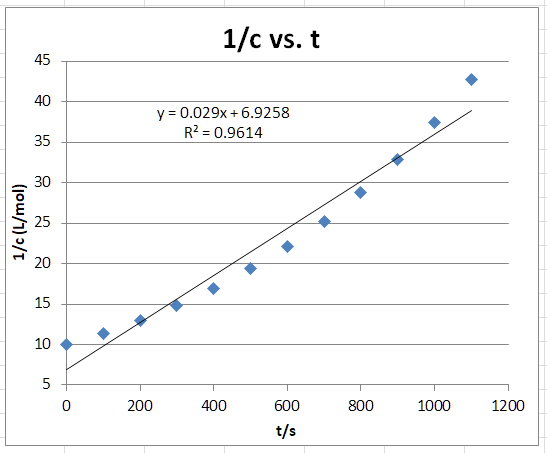
The graph appears to be a curve.
Conclusion
Your data give the best fit to a first-order rate law of the form
Jose suggested a different way to approach this, so I figured I'd share it.
The starting rate law is:
#r(t) = k["SO"_2"Cl"_2]^m#
Jose suggested that one could take the
#ln r(t) = mln["SO"_2"Cl"_2] + lnk#
But this requires that we generate a new column of data:
#r(t) = -(Delta["SO"_2"Cl"_2])/(Deltat)#
and for
#ul(ln[r(t) xx 10^4] ("M/s")" "" "" "ln["SO"_2"Cl"_2]_"mp" ("M")" ")#
#ln1.24" "" "" "" "" "" "" "" "" "ln0.0938#
#ln1.08" "" "" "" "" "" "" "" "" "ln0.0822#
#ln0.95" "" "" "" "" "" "" "" "" "ln0.0721#
#ln0.83" "" "" "" "" "" "" "" "" "ln0.0632#
#ln0.73" "" "" "" "" "" "" "" "" "ln0.0554#
#ln0.64" "" "" "" "" "" "" "" "" "ln0.0485#
You get the idea. I'll leave out the remaining
Plotting
The regression equation was found as follows using my trusty TI-83 calculator.
#"STAT"# #-># #"Edit"# , enter all the data in there. Have the#x# variable in#"L1"# and#y# variable in#"L2"# .#"STAT" -> "CALC" -> "LinReg"("ax+b")#
This gave:
#lnr(t) = 1.000765854 cdot ln["SO"_2"Cl"_2]_"mp" - 6.630082087#
This implies that the order of reaction is approx.
#lnk = -6.630082087#
and
#color(blue)(k) = e^(-6.630082087) = color(blue)("0.0013 s"^(-1))#
So this method works too. However, you can see it is a big hassle, when you have this many data points, to rewrite all of them into


