How to Calculate the Surface Area of cone with radius of 1.8cm and height of 2.4cm?
1 Answer
Explanation:
The formula for the surface area of a cone is
From the given information, we already have some of the numbers. We know that
However, we do not know the slant height of the triangle. Using this picture below as a guide, you can fill in
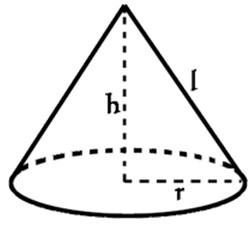
Using the Pythagorean Theorem (
We can say that
Yay! We've solved the first part. Now that we know all our variables, we can plug that into the first equation.

