How to calculate this? #int_0^piarcsin(sinx)dx.#
1 Answer
May 20, 2017
Split the integral.
Explanation:
For
For
Therefore,
Evaluate the integrals or look at the graph of
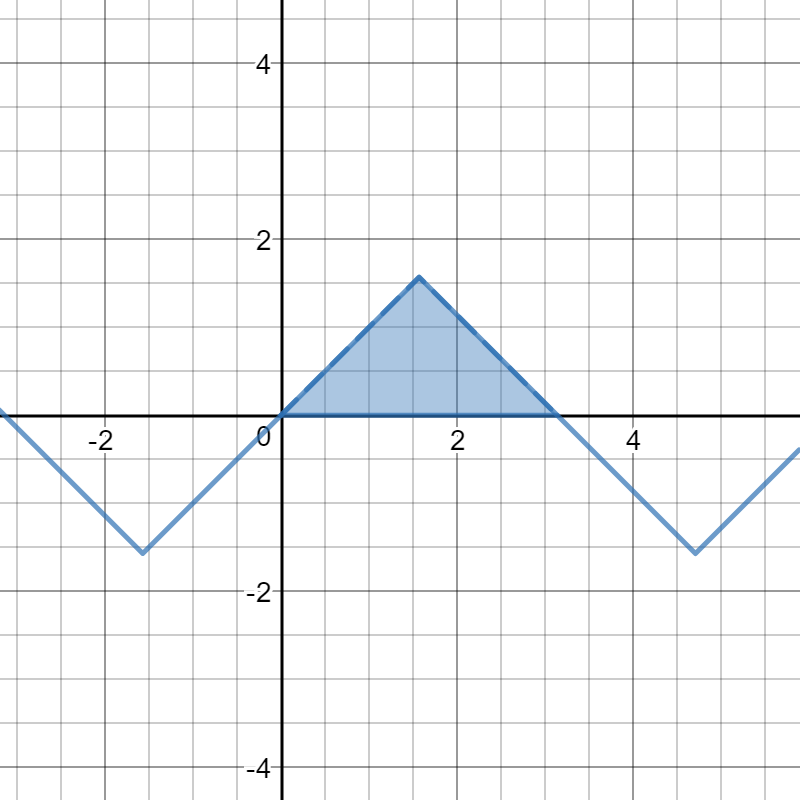
This is a triangle with base

