How to calculate triangle MNP ?
Know S triangle ABC is #24 cm^2#
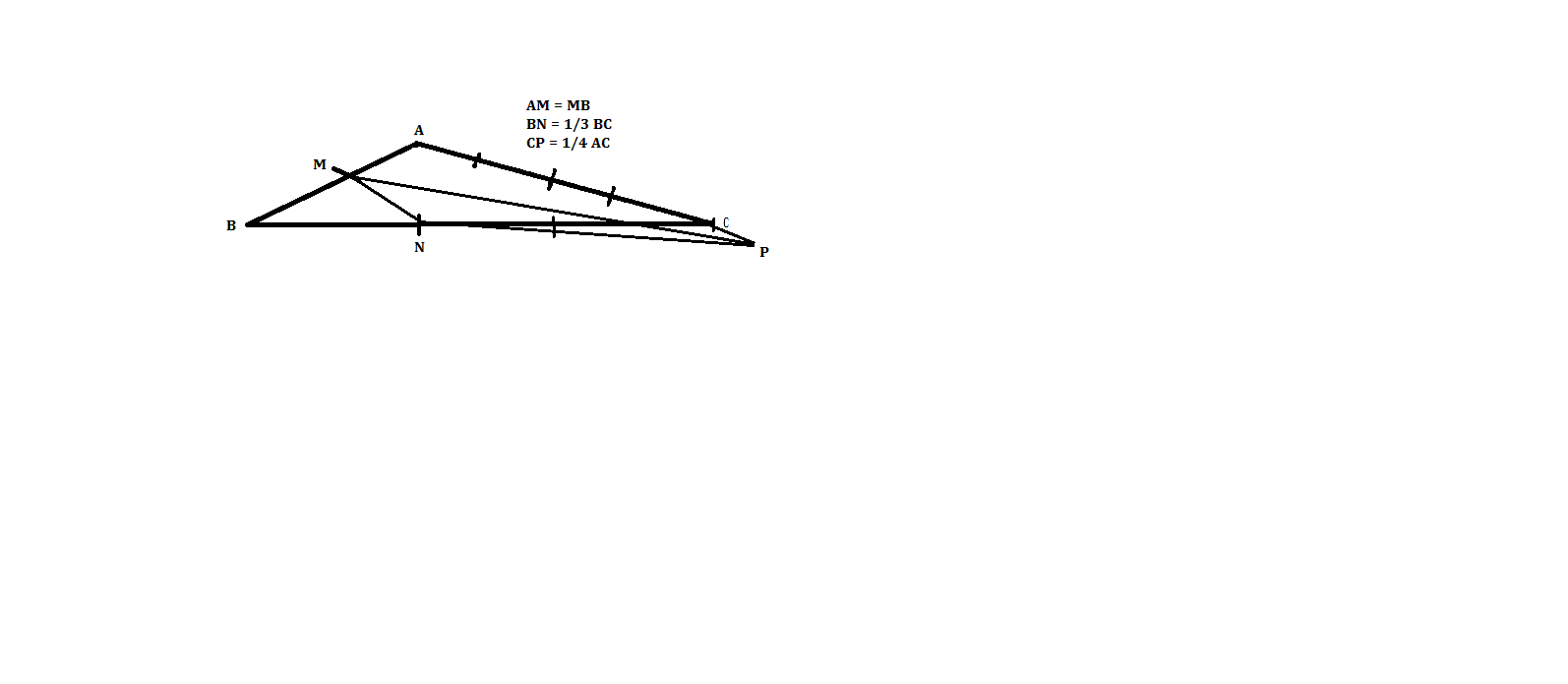
In AB, take M, know AM = MB.
In BC, take N, know BN = #1/3# BC
In the long stretch of AC, take P, know CP = #1/4# AC.
Calculate S triangle MNP.

Know S triangle ABC is
In AB, take M, know AM = MB.
In BC, take N, know BN =
In the long stretch of AC, take P, know CP =
Calculate S triangle MNP.
2 Answers
area of
Explanation:
Let
let
given
as
as
as
as
as
Now,
Area of
Explanation:
Solution 2 :
Let
see Fig 1
given
as
See Fig 2,
as
as
See Fig 3,
as
Now,
