Question

How to compare the relative change in momentum of two blocks attached by a pulley?

Two blocks A and B of equal mass are connected by a light inextensible taut string passing over two light smooth pulleys fixed to the blocks. The parts of the string not in contact with the pulleys are horizontal. A horizontal force F is applied to the block A as shown. There is no friction, then

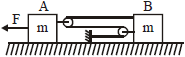
(1) the acceleration of A will be more than that of B
(2) the acceleration of A will be less than that of B
(3) the sum of rate of changes of momentum of A and B is greater than the magnitude of F
(4) the sum of rate of changes of momentum of A and B is equal to the magnitude of F

Answer 1

See below.

Explanation:

Calling `C` the string anchor point we have

`L = (x_B-x_A)+(x_B-x_A)+(x_B-x_C)` or

`L = 3x_B-2x_A-x_C` so

`0 = 3 ddot x_B-2 ddot x_A` because `x_C = C^(te)` then

`ddot x_A = 3/2 ddot x_B` ---> (1)

Now solving the system

#{(t_A = 2 t_B), (t_C = 2 t_B), (t_B + t_C = m ddotx_B), (F - t_A = m ddotx_A), (ddotx_A = 3/2 ddotx_B):}#

where `t_i, i = {A,B,C}` are string tensions, solving for `t_i, ddotx_A,ddot x_B` we obtain

#{(),(t_A -> (4 F)/13), (t_B -> (2 F)/13), (t_C -> (4 F)/13), (ddotx_A -> (9 F)/(13 m)), (ddotx_B -> (6 F)/(13 m)):}#

and comparing `F` with `m ddot x_A+m ddot x_B` we have

`F < 15/13 F` ----> (3)