How to decide which forces that works on the acceleration?
The exercise asks about finding the acceleration to the box if it has a #m = 2.35kg# .
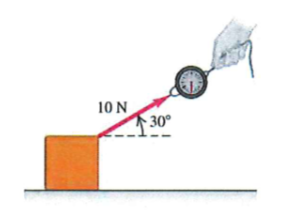
But I'm kinda unsure about how one should think about calculating the forces on the box. Since the force is neither vertical or horisontal, but rather diagonal.
I am guessing that Newton's second law will be the right approach to this exercise, #∑F=ma# . But how do I decide the forces here, since the force is diagonal?
If someone could help me with a logical explaination and not only the answer I would really appreciate it.
The exercise asks about finding the acceleration to the box if it has a

But I'm kinda unsure about how one should think about calculating the forces on the box. Since the force is neither vertical or horisontal, but rather diagonal.
I am guessing that Newton's second law will be the right approach to this exercise,
If someone could help me with a logical explaination and not only the answer I would really appreciate it.
2 Answers
Explanation:
When looking at a diagonal force, the angle can be used to break down the diagonal force into the horizontal and vertical components of that force, using sine and cosine.
Since we want to find the acceleration to the right, we would use the force of
The answer is in the Explanation.
Explanation:
The problem does not say anything about friction ... fortunately. It is fortunate because when friction is involved in a more advanced question you will see that the angle complicates matters significantly.
You probably have learned about forming a resultant vector from 2 separate forces working on the same object. What is needed here is to do the reverse -- where the 10 N is the resultant of a vertical force and a horizontal force. Draw the given vector and draw the 2 vectors that could have been the given forces in a "finding the resultant" problem. Then use your trigonometry skills.
#sin30^@ = F_y/(10 N)#
Solve for#F_y# . This force is vertical and is not used in this problem.
#cos30^@ = F_x/(10 N)#
Solve for#F_x# . This force is horizontal and, since the box will move horizontally, is the force to plug into Newton's 2nd.
I hope this helps,
Steve


