Suppose that, intt^2/sqrt(a+2t^5)dt=f(t)+c.
:." by the Definition of Integral, "f'(t)=t^2/sqrt(a+2t^5)......(star).
Further, using the Fundamental Theorem of Calculus, we have,
int_0^xt^2/sqrt(a+2t^5)dt=f(x)-f(0).............................(starstar).
Now, lim_(x to 0){int_0^xt^2/sqrt(a+2t^5)dt}/(bx-esinx),
=lim_(x to 0){f(x)-f(0)}/{x(b-e*sinx/x)}............[because, (starstar)],
=lim_(x to 0){(f(x)-f(0))/(x-0)}/{(b-e*sinx/x)},
={lim_(x to 0)(f(x)-f(0))/(x-0)}/{lim_(x to 0)(b-e*sinx/x)},
=(f'(0))/(b-e*1).
Here, by (star), f'(0)=0^2/sqrt(a+2*0^5)=0.
:. lim_(x to 0){int_0^xt^2/sqrt(a+2t^5)dt}/(bx-esinx)=0.
This means that, there do not exist a, b in RR, such that the
limit in question be 1/pi.
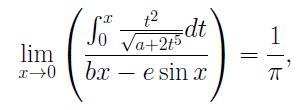 limit
limit limit

