How to determine height of the cylinder with maximum volume engraved in a sphere with radius #R#?
3 Answers
Explanation:
This problem is really interesting, but will definitely require some visualization to figure out. Let's start by using the formula for the volume of a cylinder:
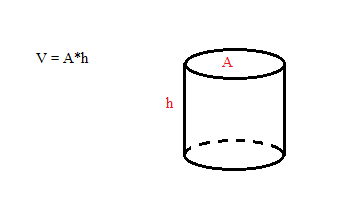
We know that the area of a circle is:
Therefore, the volume is:
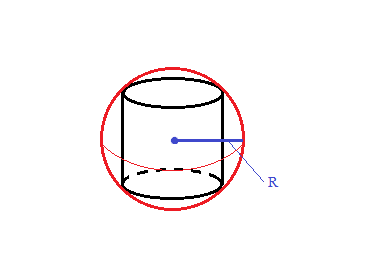
This cylinder, however, is engraved in a sphere. Its cross-sectional area and height are, therefore, restricted by the sphere as shown below:
Now, imagine cutting the sphere in half two times. After the first and second cuts, we will see:
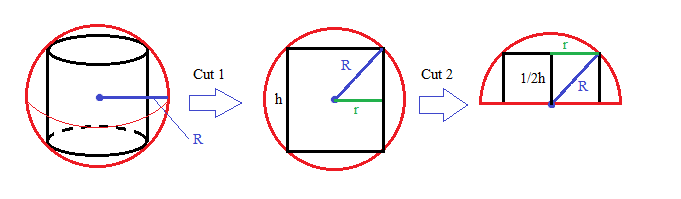
If we focus on the cross section in the last cut, we can use the Pythagorean theorem to find a relationship between
Solving for
Now that we have
Simplify the expression:
Now that we have the volume of the cylinder expressed as a function of its height,
(Recall: Local maximum of a function is located where its derivative equals 0).
Therefore, the value of
Explanation:
Assuming a cylinder with the vertical axis coincident with the
we have
but
so
or
The solutions are
so
NOTE: This is a maximum point because
See the answer below:
This problem has been translated and adapted from the same problem shown in the website http://ecalculo.if.usp.br/derivadas/estudo_var_fun/probl_otimizacao/problemas/problema11.htm
Thanks to the students of Mathematics at USP, University of São Paulo who developed this course in Mathematics as a conclusion paper and posted at http://ecalculo.if.usp.br/.
Explanation:
See the answer below:
This problem has been translated and adapted from the same problem shown in the website http://ecalculo.if.usp.br/derivadas/estudo_var_fun/probl_otimizacao/problemas/problema11.htm
Thanks to the students of Mathematics at USP,University of São Paulo who developed this course in Mathematics as a conclusion paper and posted at http://ecalculo.if.usp.br/.



