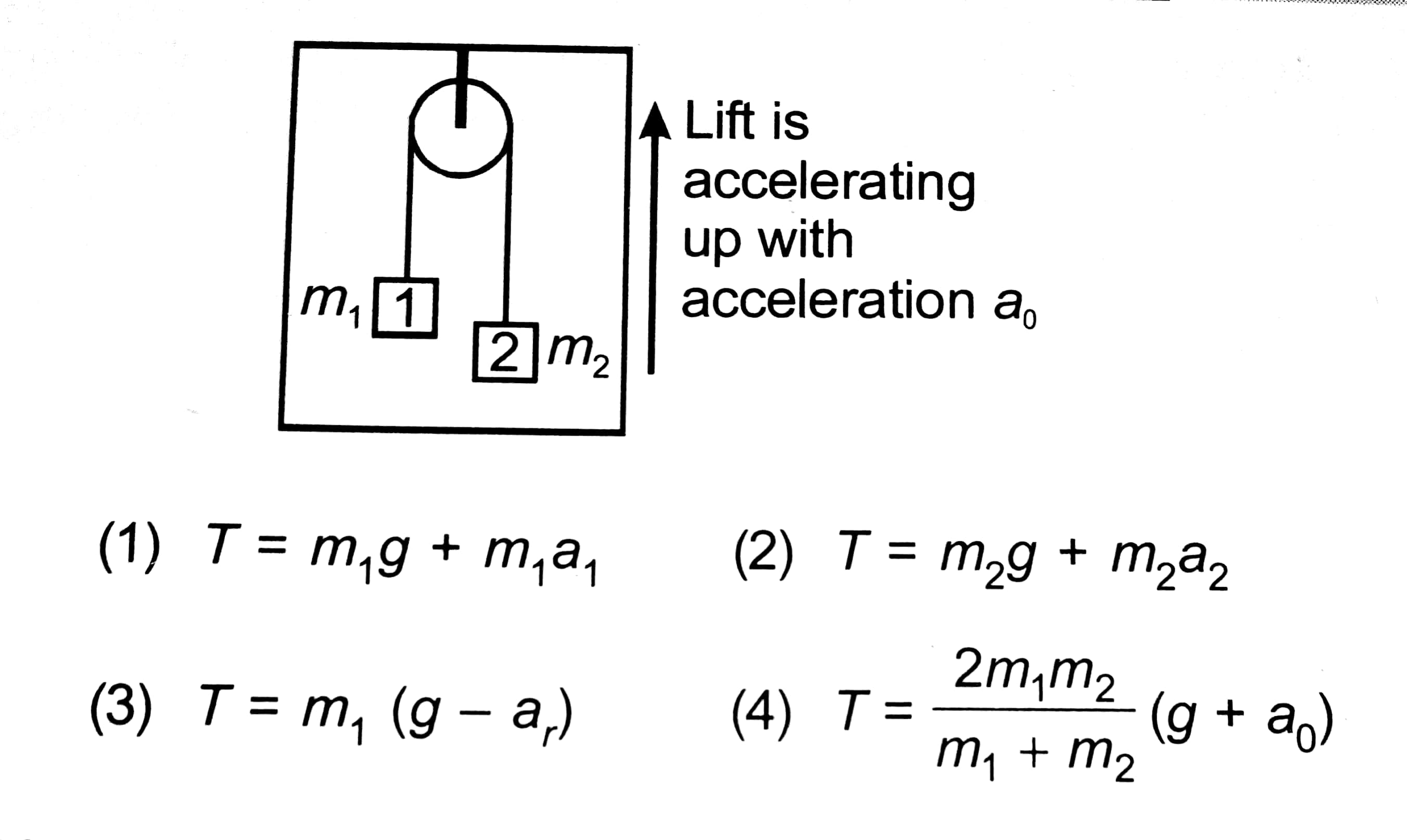
How to do 187th question?
2 Answers
See below.
Explanation:
Considering the rope length
We have
now deriving twice
but
Solving those equations we obtain
we leave the conclusions to the reader.
The question asks for each one is Incorrect...
(4)
Explanation:
As general statement:
Since
Here's the formula for tension of two masses:
Substitute for
Number 2 is correct
Substitute for
Number 1 is also correct
Number 3 however refers to the MAGNITUDE of relative acceleration in comparison to the pulley, so we can add to our statement:
Substitute for
Number 3 is also correct
Number 4 is incorrect because:
going back to:
Solve for
So:


