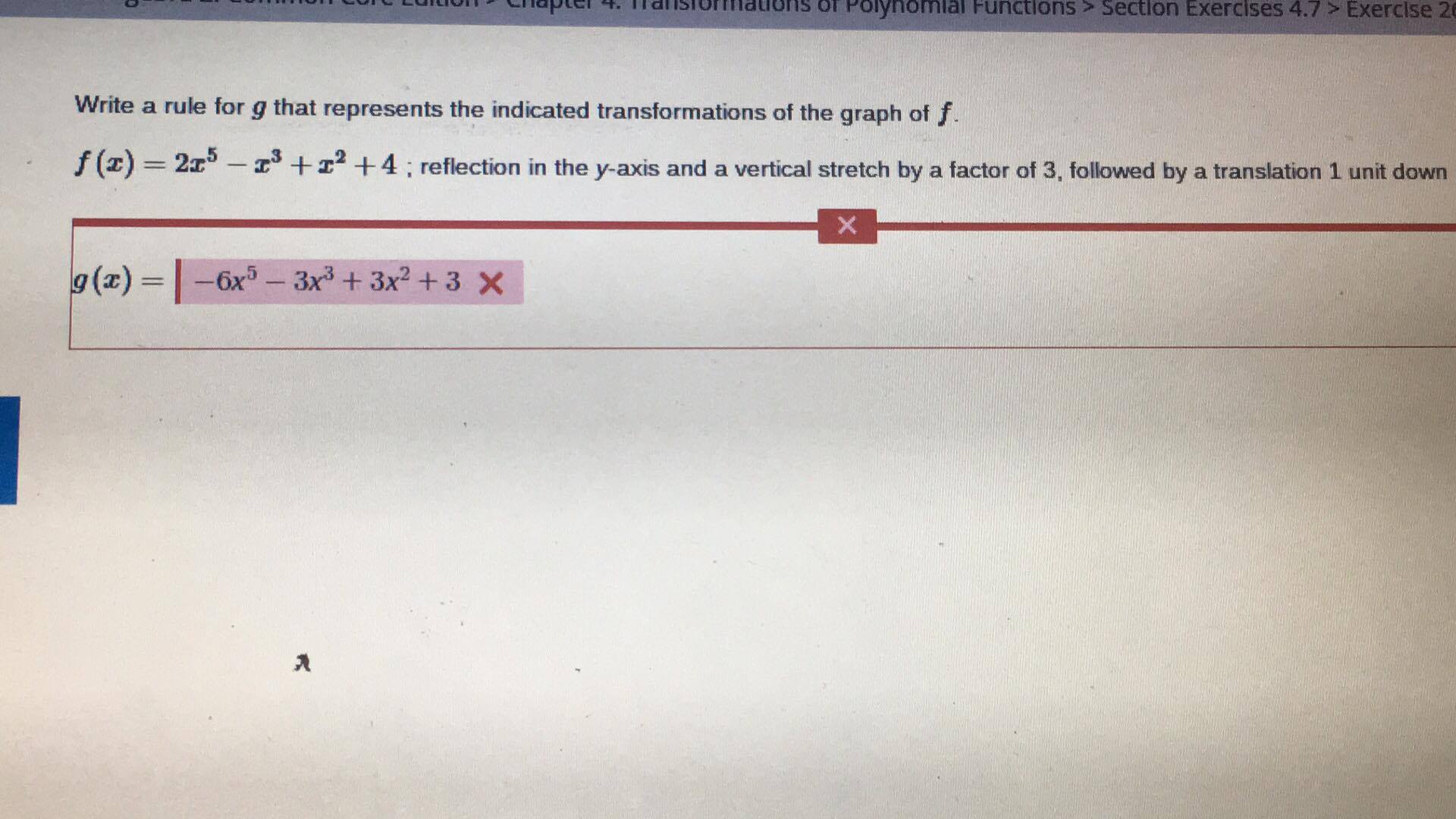
Given: #f(x)=2x^5-x^3+x^2+4#
Target to achieve: #g(x)=color(green)(-6x^5-3x^3+3x^2+3)#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Consider the first term in #f(x)# which is #2x^5#
We need to change this into #-6x^5# and this can be achieved by using: #(-3)xxf(x)# It will change all the other terms in #f(x)# but we can adjust them as we go along.
#+2x^5-x^3+color(white)("d")x^2+4#
#ul(color(white)("ddddddddddddd.d")-3)larr"Multiply"#
#-6x^5+3x^3-3x^2-12#
We now have the target #x^5# term #->-3f(x)# but the rest does not match the target. Thus we determine the adjustment by applying a subtraction.
Target#color(white)(".")->-6x^5-3x^3+3x^2+3#
#-3f(x) ->ul(-6x^5+3x^3-3x^2-12larr" Subtract")#
#color(white)("dddddddddddd")color(red)(0-6x^3+6x^2+15)#
Giving #color(white)("d")-3f(x)color(red)(-6x^3+6x^2+15larr" The adjustment")#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Check")#
#-3f(x)->color(white)("dddddd")-6x^5+3x^3-3x^2-12#
The adjustment #-> ul(color(white)("dddddd")color(red)(-6x^3+6x^2+15)larr" Add")#
#color(white)("dddddddddddddddd")-6x^5-3x^3+3x^2+3#
The target #->color(white)("ddddd")color(green)(-6x^5-3x^3+3x^2+3) #
A perfect match so #-3f(x) -6x^3+6x^2+15# is correct