How to do this perpendicular bisector of a chord question?
Unable to figure this out and the answer gives no explanation in the textbook. Could someone kindly help?

Unable to figure this out and the answer gives no explanation in the textbook. Could someone kindly help?
3 Answers
The center of the circle is
Explanation:
The equation of a circle is
where
and
Plug in the equation of the circle for the 3 coordinates
Point A
Point B
Point C
From equations 1 and 2, we get
From equation 2 and 3, we get
From equation
Therefore,
the centre of the circle is
The radius of the circle is
(3, 3 )
Explanation:
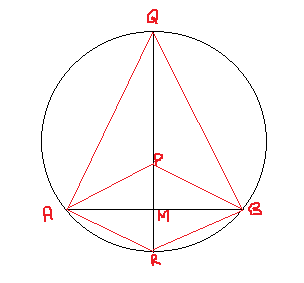
Here AB is a chord, o is the center of the circle. OD is the perpendicular of the chord.Three points A, B and C may be the points of a triangle ABC which is inscribed of a circle.we have to find out the co-ordinates of o.
Rest procedure as above done.
As explained below
Explanation:
Perpendicular bisector of a chord of a circle passes through the centre.
To prove this, draw a chord AB of a circle. If M is the midpoint of AB, the perpendicular bisector would passe through M. Now take any point P on this perpendicular bisector. Join A and B with P.
Now consider the right triangles APM and BPM. Both these triangles would be congruent by SAS, because AM=BM, PM=PM and angle AMP= angle BMP=
Therefore AP=BP. Since P is any point on the perpendicular bisector, it can be concluded that all points on the perpendicular bisector would be equidistant from A and B.
Now extend the perpendicular bisector on either side of chord AB, so that it meets the circle at points Q and R. Then AQ= BQ and AR=BR. The two triangles thus formed AQR and BQR would be congruent by SSS because AQ=BQ, AR=BR and QR=QR. Thus angle QAR = angleQBR. Since AQBR is a cyclic quadrilateral, angles QAR and QBR will be supplementary. These two angles would thus be
Thus it is proved that perpendicular bisector of the chord AB passes through the centre of the circle.