Question

How to draw the region R whose area is given by the iterated integral. Then change the integration order and show that both orders give the same area? With step by step solution please?

`int_0^2int_0^(x)dydx+int_2^4int_0^(4-x)dydx`

Answer 1

`int_0^2 \ int_0^x \ dy \ dx + int_2^4 \ int_0^(4-x) \ dy \ dx = 4`

Explanation:

We seek:

`I = I_1+I_2`, where `I_1=int_0^2int_0^(x)dydx`, `I_2=int_2^4int_0^(4-x)dydx`

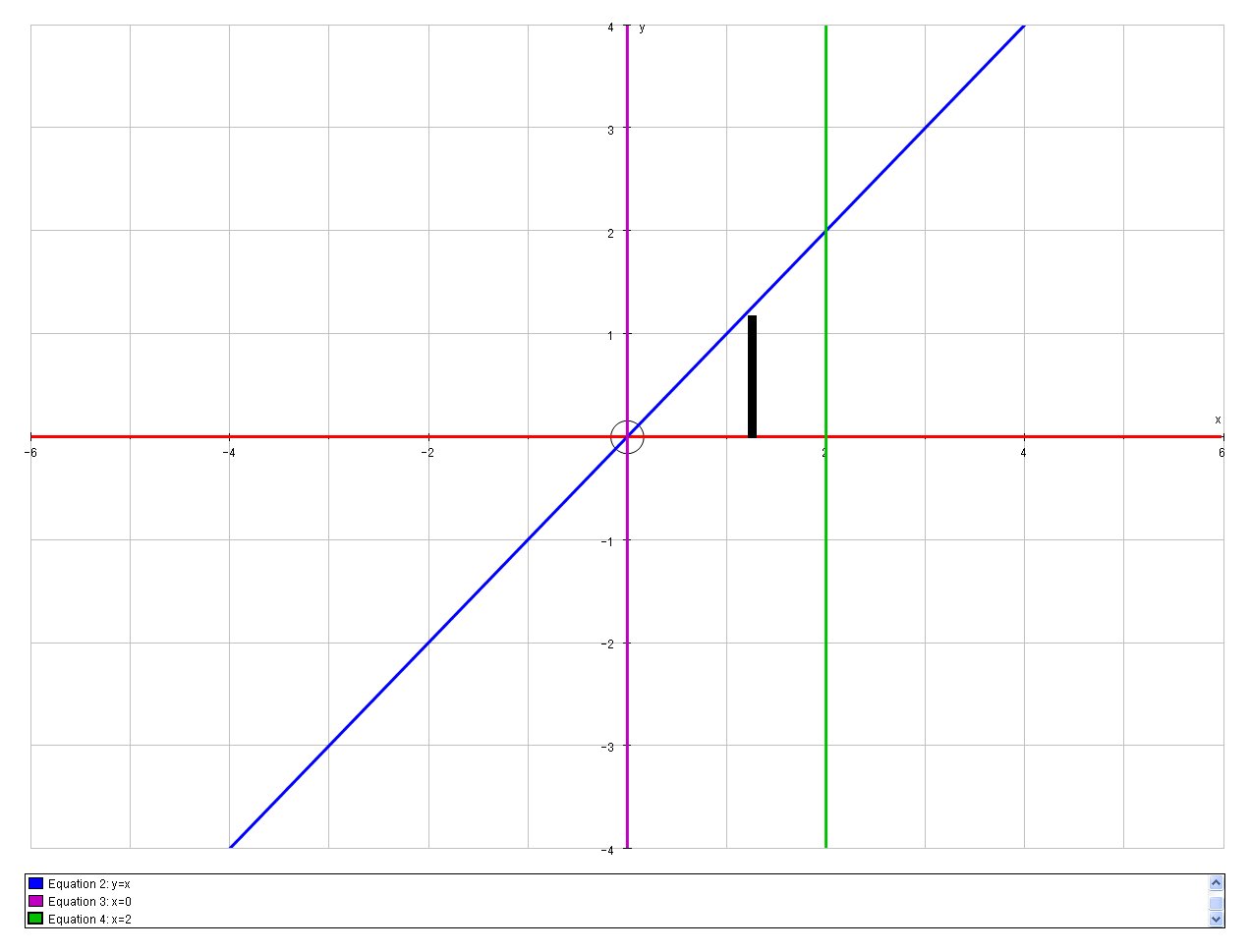
Consider the First Integral:

The regions of the integral are as follows:

Where we sum first from `y=0` to `y=x` then from `x=0` to `x=2` yielding:

`I_1 = int_0^2 \ int_0^(x) \ dy \ dx`
`\ \ \ = int_0^2 \ [ \ y \ ]_0^(x) \ dx`
`\ \ \ = int_0^2 \ (x-0) \ dx`
`\ \ \ = [ \ x^2/2 \ ]_0^2`
`\ \ \ = 1/2(4-0)`
`\ \ \ = 2`

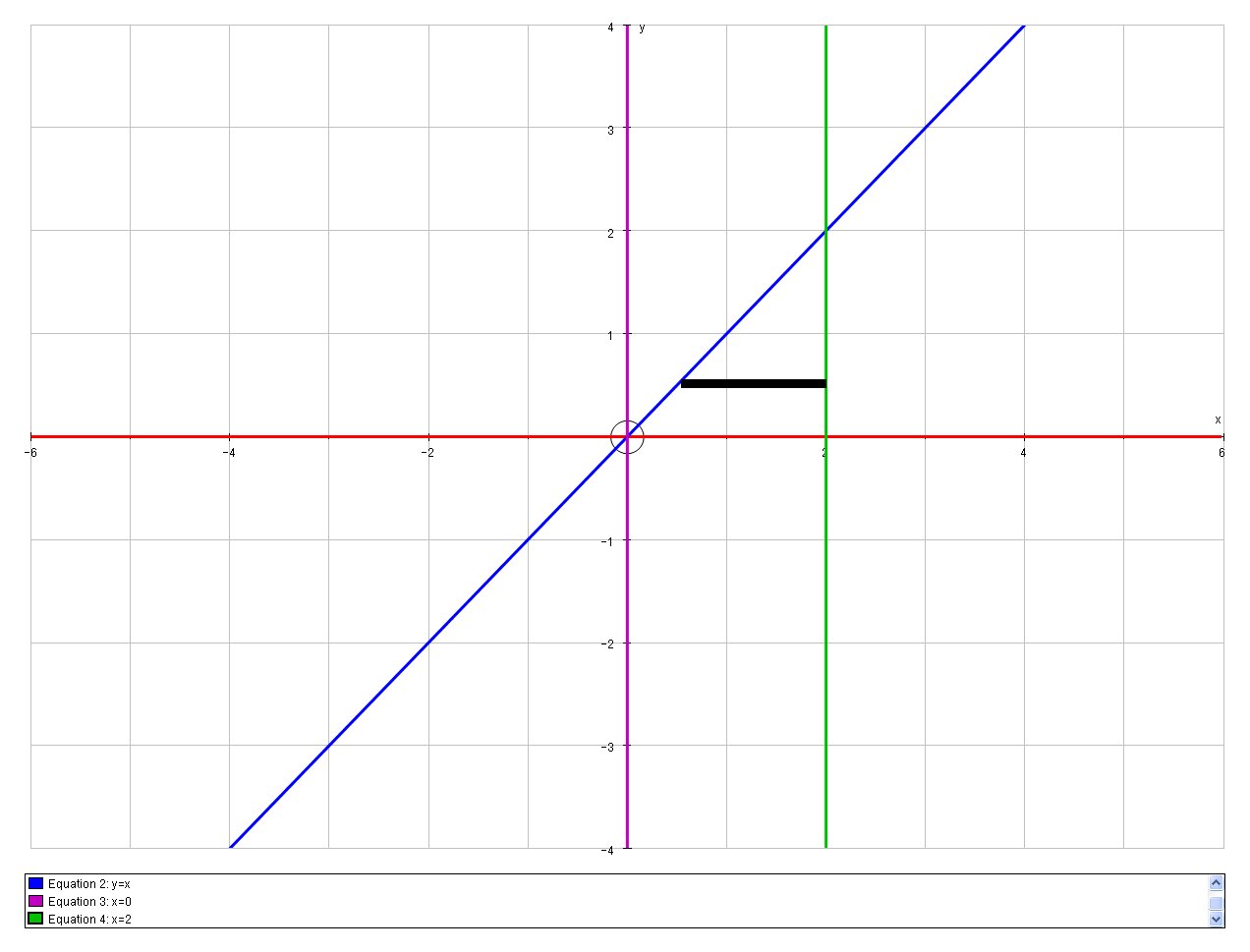
And if we reverse the order of integration:

We now sum first from `x=y` to `x=2` as `(y=x iff x=y)` then from `y=0` to `y=2`, Allowing us to write:

`I_1 = int_0^2 \ int_y^2 \ dx \ dy`
`\ \ \ = int_0^2 \ [ \ x \ ]_y^2 \ dy`
`\ \ \ = int_0^2 \ (2-y) \ dy`
`\ \ \ = [2y-y^2/2]_0^2`
`\ \ \ = (4-2) - (0-0)`
`\ \ \ = 2`, as before

|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

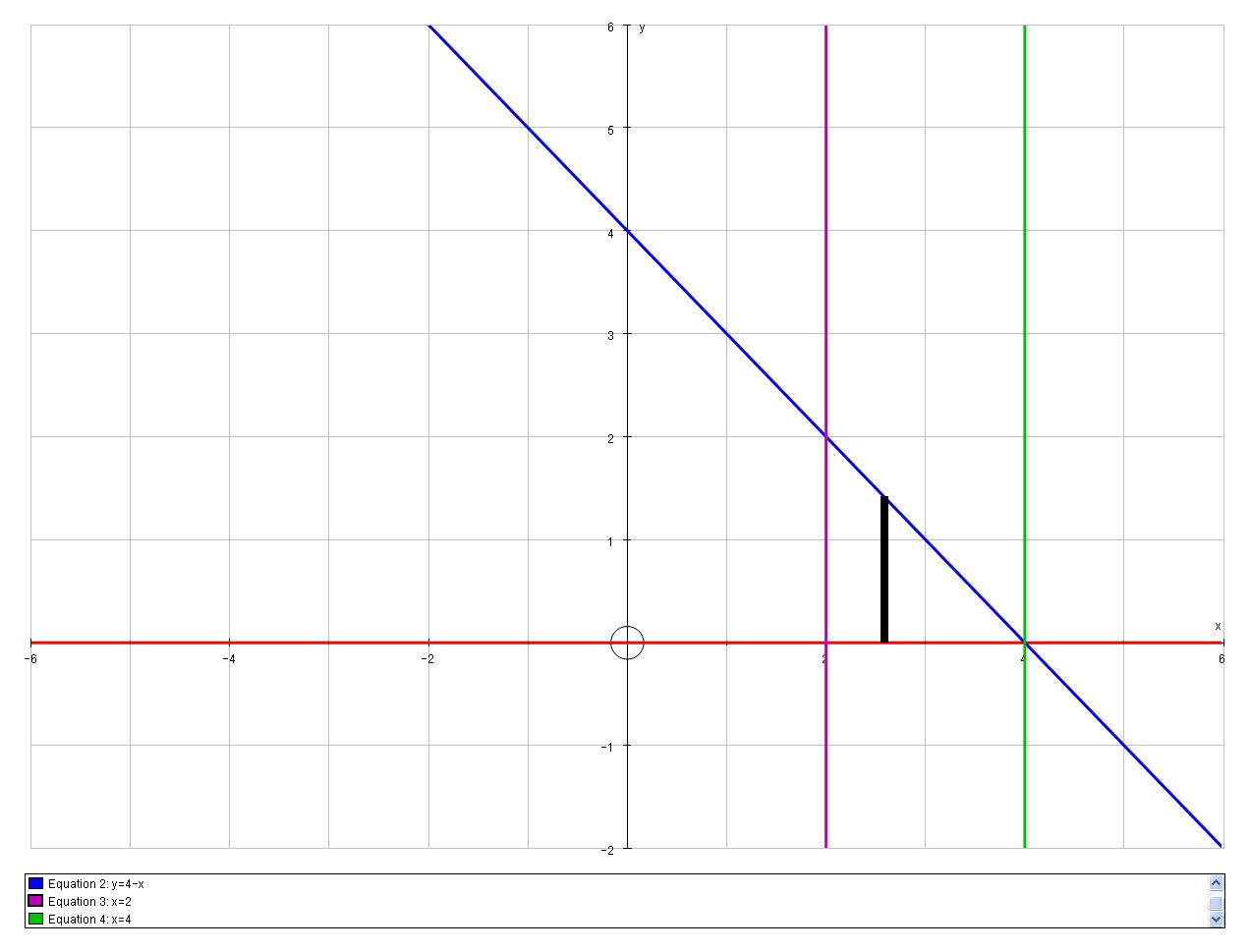
Consider the Second Integral:

The regions of the integral are as follows:

Where we sum first from `y=0` to `y=4-x` then from `x=2` to `x=4` yielding:

`I_2 = int_2^4 \ int_0^(4-x) \ dy \ dx`
`\ \ \ = int_2^4 \ [ \ y \ ]_0^(4-x) \ dx`
`\ \ \ = int_2^4 \ (4-x)-(0) \ dx`
`\ \ \ = [ \ 4x - x^2/2 \ ]_2^4`
`\ \ \ = (16-8) - (8-2)`
`\ \ \ = 8- 6`
`\ \ \ = 2`

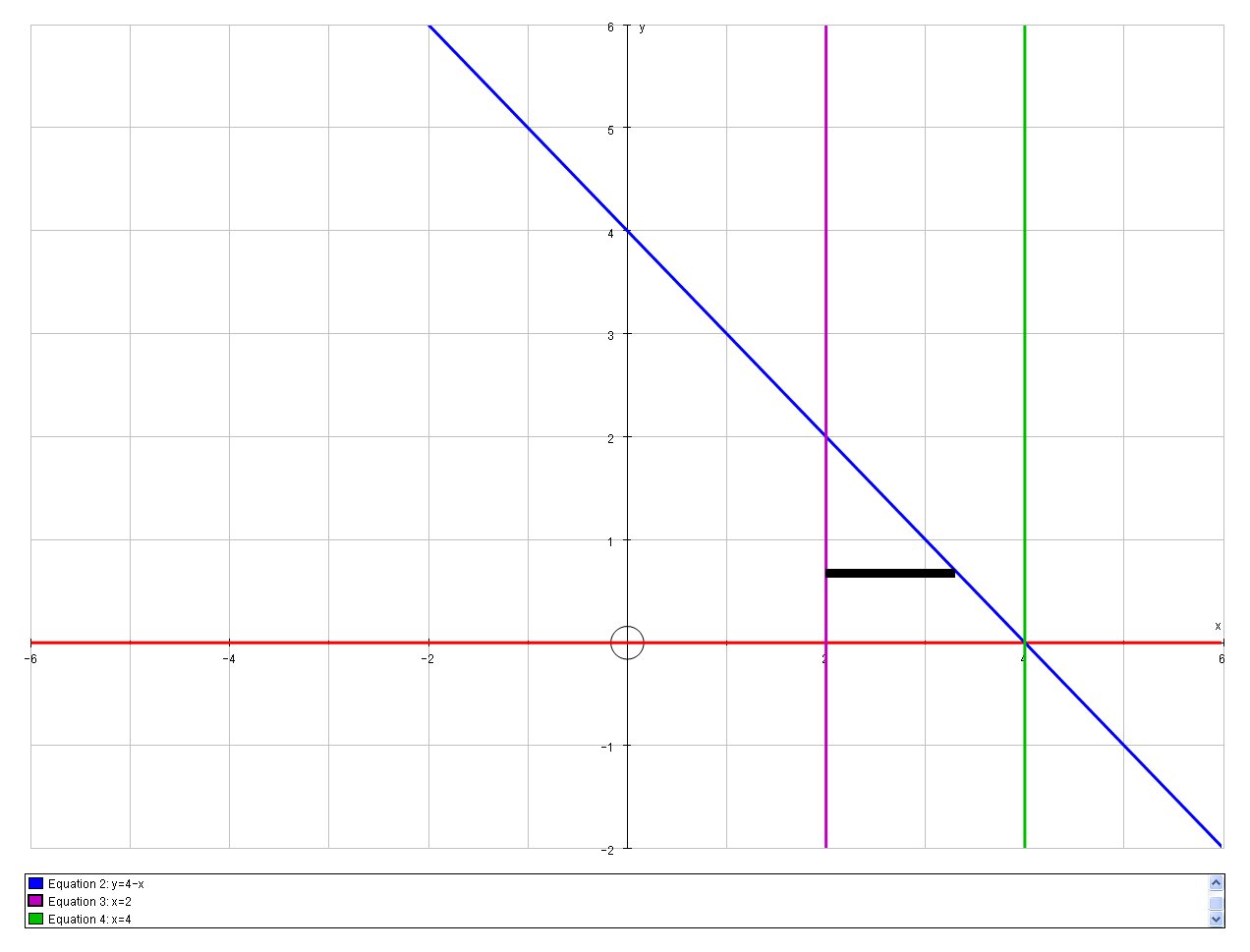
And if we reverse the order of integration:

We now sum first from `x=2` to `x=4-y` as `(y=4-x iff x=4-y)` then from `y=0` to `y=2`, Allowing us to write:

`I_2 = int_0^2 \ int_2^(4-y) \ dx \ dy`
`\ \ \ = int_0^2 \ [ \ x \ ]_2^(4-y) \ dy`
`\ \ \ = int_0^2 \ (4-y)-(2) \ dy`
`\ \ \ = [ \ 2y-y^2/2 \ ]_0^2 \`
`\ \ \ = (4-2) - (0)`
`\ \ \ = 2`, as before.

|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

Summary

Combining the results, irrespective of the order of integration, we have:

`I = int_0^2 \ int_0^x \ dy \ dx + int_2^4 \ int_0^(4-x) \ dy \ dx`
`\ \ = I_1 + I_2`
`\ \ = 2 + 2`
`\ \ = 4`