How to find area bounded by a curve and a line?
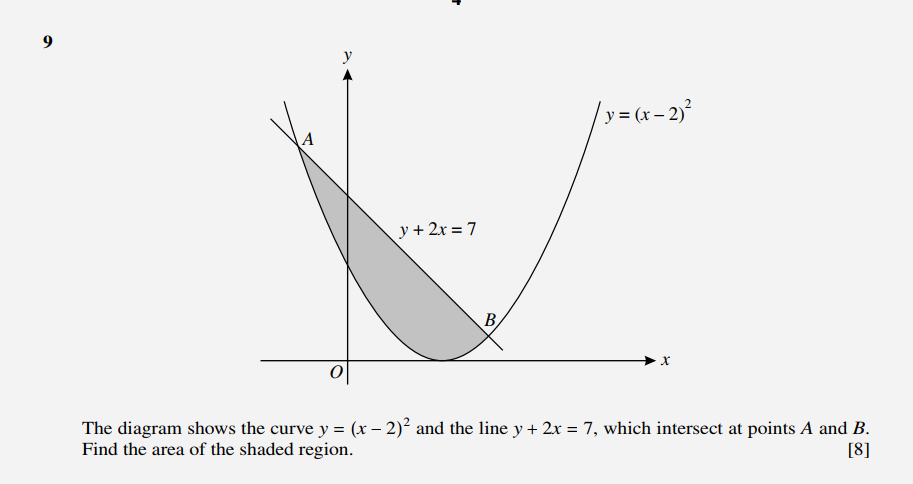
The points of intersection of the line and the curve are ( -1 , 9 ) and ( 3 , 1 )
The points of intersection of the line and the curve are ( -1 , 9 ) and ( 3 , 1 )
1 Answer
Aug 15, 2017
Explanation:
In your case, the diagram shows that f(x) is the line but we must write is as y in terms of x:
The quadratic is g(x):
Expand the square:
You have provided the limits of integration by giving the x coordinates where the functions intersect:
Start with the equation:
Substitute the values of
Before we integate, I shall simplify the integrand:
Integrate
Evaluate at the limits:
