Question

How to do this?

equations of the normals to the curve
`y=2^x - 7` at the points where `x=1`and `x=-1.` calculate the coordinates of the point of intersection of these normals.

Answer 1

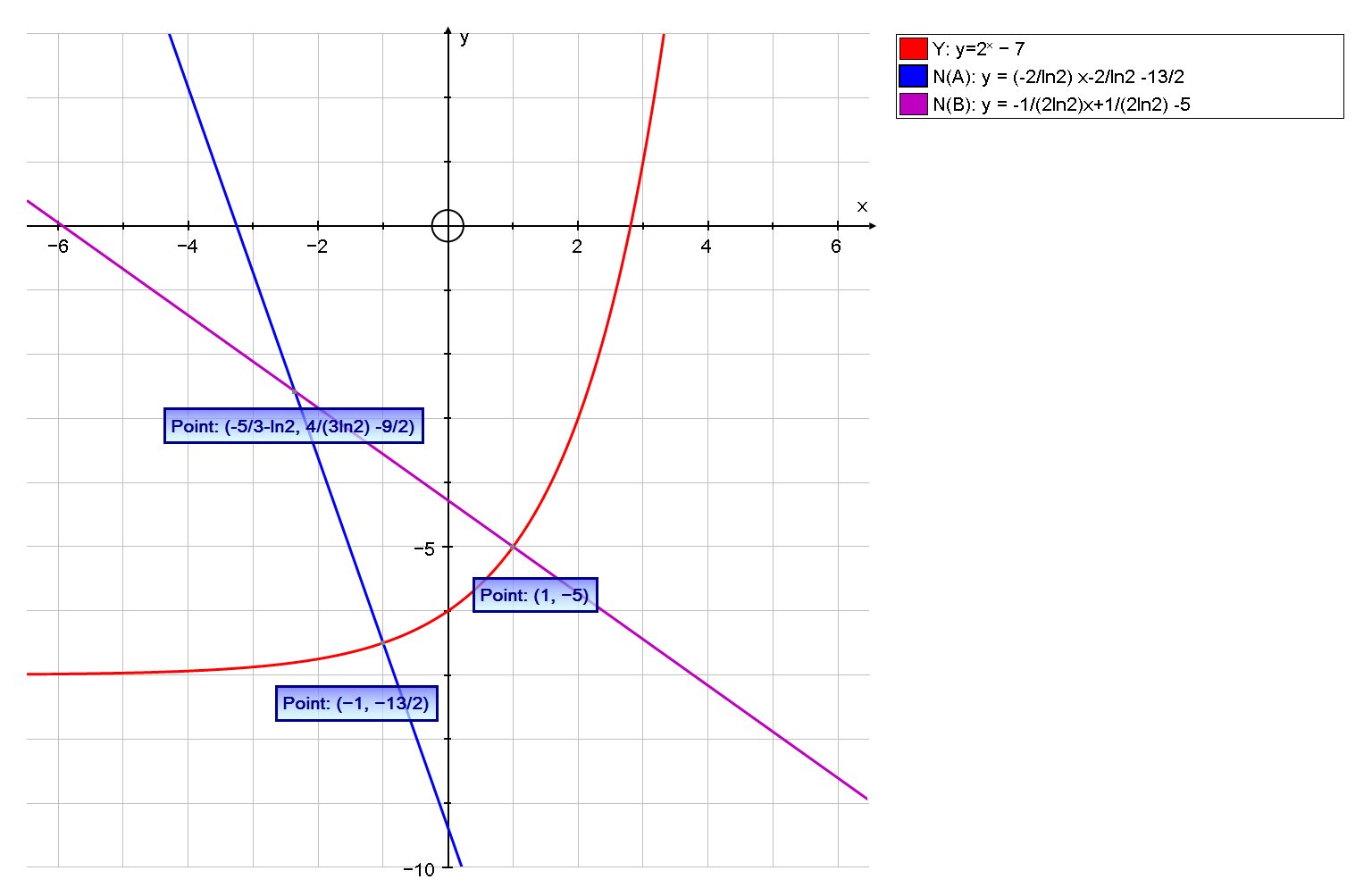
The Normals at `-1` and `1` meet at the point with coordinates:

`(-5/3-ln2, 4/(3ln2) -9/2)`

Explanation:

The gradient of the tangent at any particular point on the function is given by the derivative at that point. The normal is perpendicular to the tangent, so their products will be `-1`.

`y=2^x -7`

Differentiating wrt `x` we get;
`dy/dx = (ln2)2^x`

When
`x=-1 => y=2^-1 -7 = -13/2`
`x=1 \ \ \ \ \ => y=2^1-7 \ \ \ =-5`

Let `{ (A = (-1, -13/2)), (B=(1,-5)) :}`

At A:
gradient of tangent `= (ln2)2^-1 = 1/2ln2`
gradient of normal `= -2/ln2`

So normal passes through `(-1, -13/2)` and has gradient `-2/ln2`, so using `y-y_1=m(x-x_1)` the equation is;

`y - (-13/2) = -2/ln2(x-(-1))`
`y +13/2 = -2/ln2x-2/ln2`
`y = -2/ln2x-2/ln2 -13/2` ..... [1]

At B:
gradient of tangent `= (ln2)2^1 = 2ln2`
gradient of normal `= -1/(2ln2)`

So normal passes through `(1, -5)` and has gradient `-1/(2ln2)`, so using `y-y_1=m(x-x_1)` the equation is;

`y - (-5) = -1/(2ln2)(x-1)`
`y +5 = -1/(2ln2)x+1/(2ln2)`
`y = -1/(2ln2)x+1/(2ln2) -5` ..... [2]

Point of Intersection
Eq [1] = Eq[2] we get

`-2/ln2x-2/ln2 -13/2 = -1/(2ln2)x+1/(2ln2) -5`

Multiply by `2ln2`
`:. -4x-4 -13ln2 = -1x+1 -10ln2`
`:. -3x = 5+3ln2`
`:. x = -5/3-ln2`

Subs into Eq [2]:
`y = -1/(2ln2)(-5/3-ln2)+1/(2ln2) -5`
`y = 5/(6ln2)+1/2+1/(2ln2) -5`
`y = 4/(3ln2) -9/2`

We can confirm this graphically: