How to find out when the derived graph>0?
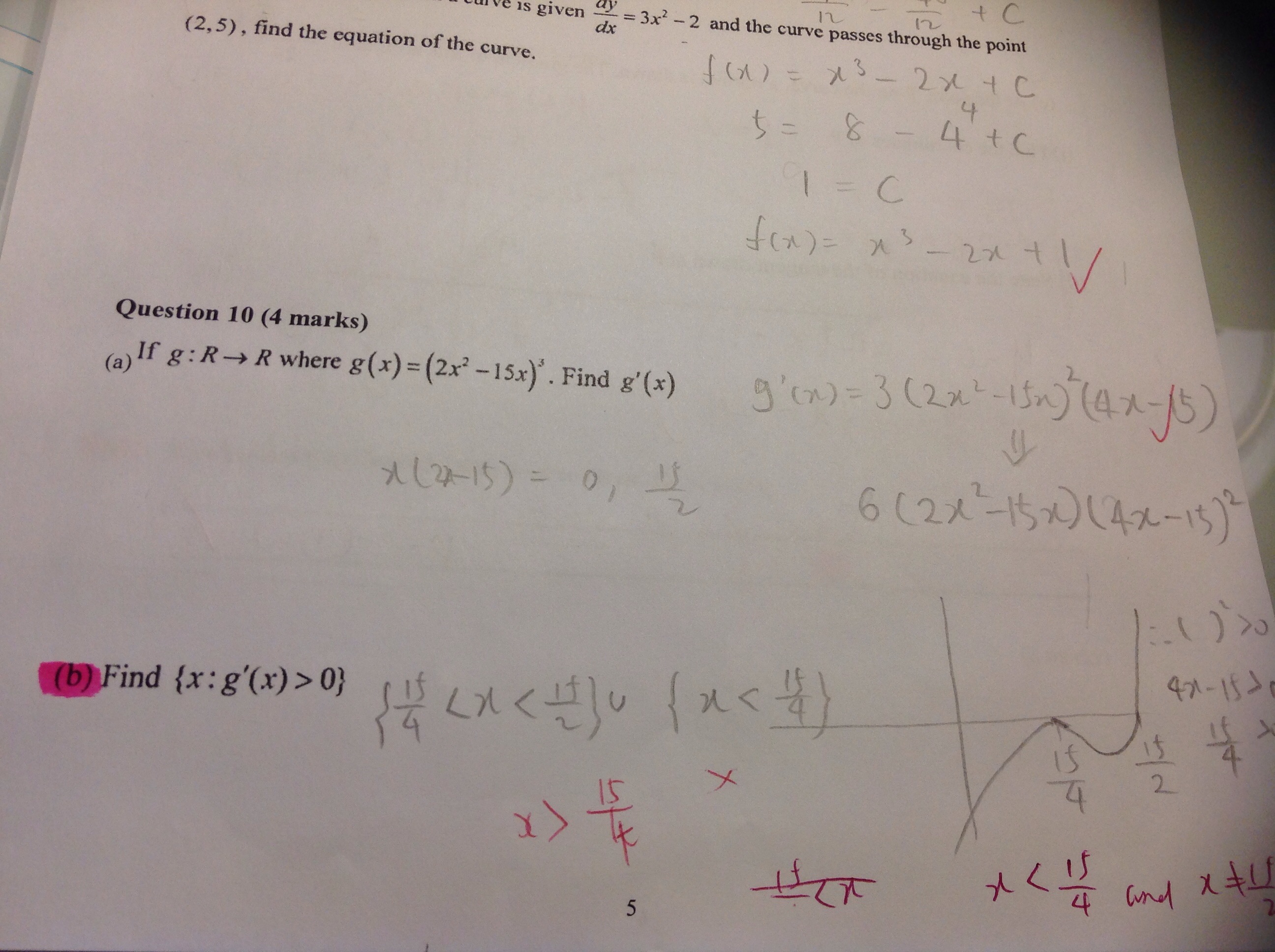
Can someone please explain to me how to do question 10 b? Thanks!
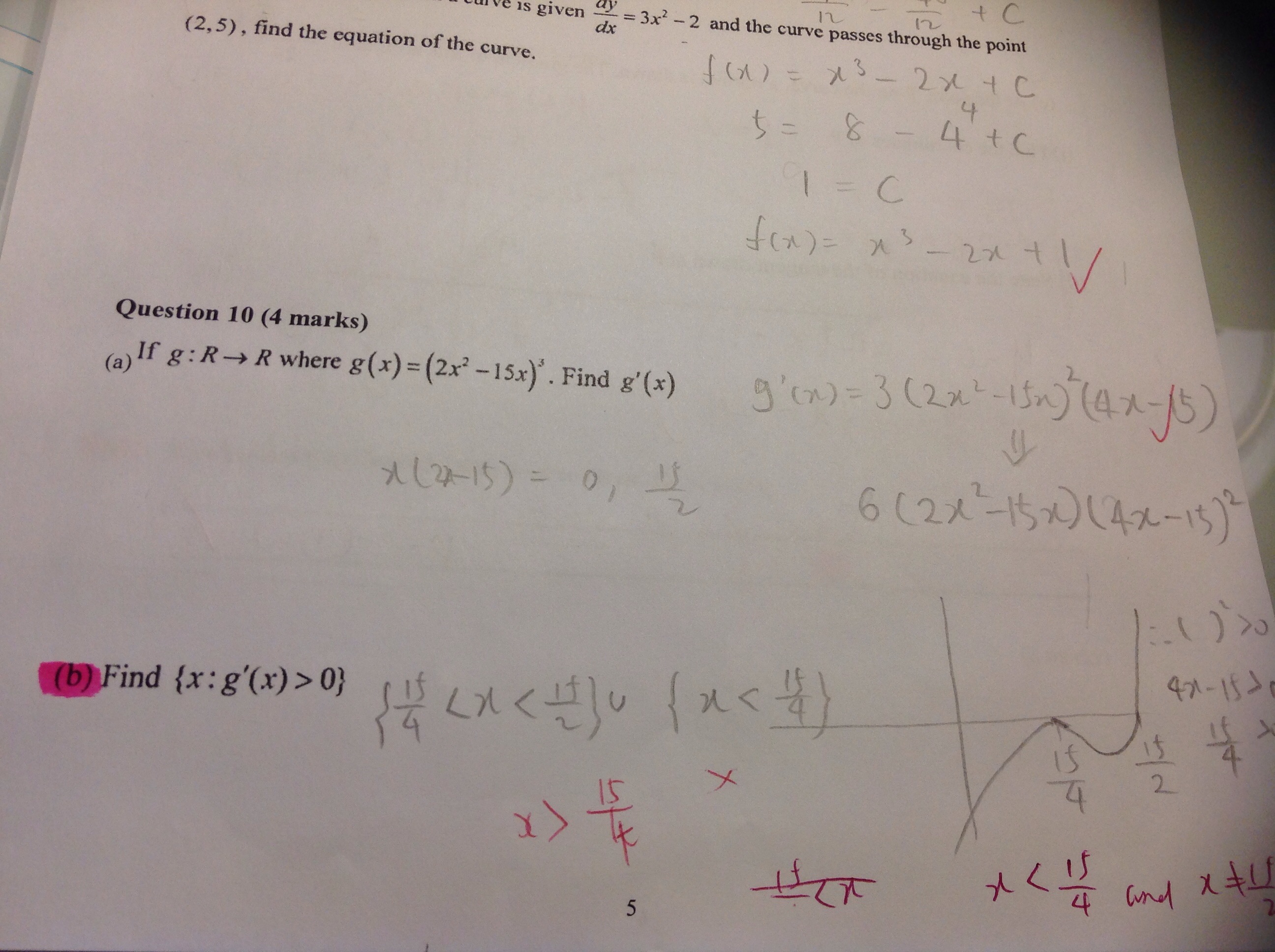
Can someone please explain to me how to do question 10 b? Thanks!
1 Answer
I believe,
Explanation:
This is tricky.
Of course the actual differentiation is no problem.
Solving part b is made simpler by simplifying
Now you know that the graph of
The shape of a standard negative quintic (=degree 5 polynomial? I don't know) comes down from a greatly positive
If you have access to a calculator, you can solve for
Since we know the shape of the curve, we know that
Hence,
Hope this helps!

