How to find potential from 2 charges through 4 points?
Could someone help with this assignment please?
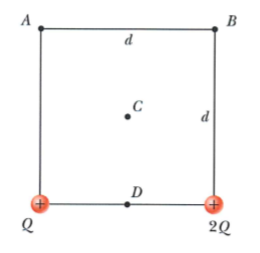
The figure shows two positive charges, Q and 2Q. They are creating an electric potential through the points of A, B, C and D. Write down the following; Which point has the highest, second highest, second lowest and lowest potential.
Could someone help with this assignment please?
The figure shows two positive charges, Q and 2Q. They are creating an electric potential through the points of A, B, C and D. Write down the following; Which point has the highest, second highest, second lowest and lowest potential.

1 Answer
May 9, 2018
Explanation:
Since the potential caused by a positive charge falls off with the distance, this problem can be worked out without any explicit calculation.
- Point D has the highest potential, being closest to both the charges
- point C comes next
- among A and B, B has the higher potential, since it is closer to the bigger charge than A
To verify, here are the actual values
#V_D= 1/(4pi epsilon_0)(Q/(d/2)+(2Q)/(d/2))=1/(4pi epsilon_0)(6Q)/d# #V_C= 1/(4pi epsilon_0)(Q/(d/sqrt2)+(2Q)/(d/sqrt2))=1/(4pi epsilon_0)(3sqrt2 Q)/d# #V_B= 1/(4pi epsilon_0)(Q/(sqrt2 d)+(2Q)/(d))=1/(4pi epsilon_0)((4+sqrt2) Q)/(2d)# #V_B= 1/(4pi epsilon_0)(Q/( d)+(2Q)/(sqrt2 d))=1/(4pi epsilon_0)((1+sqrt2) Q)/(d)#

