How to find sum of the given series?
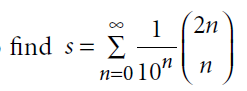
1 Answer
Jul 11, 2018
Explanation:
From the binomial expansion of
we see that the coefficient of
Thus
and so
So, our sum
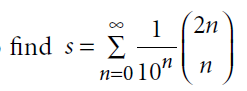
From the binomial expansion of
we see that the coefficient of
Thus
and so
So, our sum