Question

How to find the area of this shape?

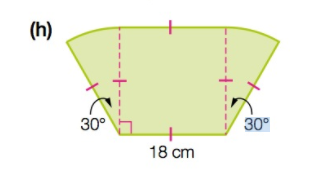
I don't know how knowing the angles can help me solve this equation. If it is not a problem, could someone explain this to me?

Answer 1

See below...

Explanation:

Firstly, all of the lines with a dash are equal in length `therefore 18cm`

Secondly , the area of the square is `18 * 18= 324cm^2`

To work out the area of the sectors, the most simplest way to do it is by using radians.

Radians are another form of measurement for angles.

1 radian happens when the radius is equal to the Arc length.

To convert to radians we do `(degrees *pi)/180`

`therefore` the angle in radians is `(30 * pi)/180 = pi/6`

Now the area of a sector is equal to `1/2 * radius^2 * angle`

Where the angle is in radians.

Here the radius of the semi circles is `18cm`

`therefore` 1 sector area is `1/2 * 18^2 * pi/6 = 27pi cm^2`

As we have two sectors we have another `27pi cm^2`

`therefore` total area `= 324 + 27pi + 27pi = 493.646...cm^2`

`approx 493.65 cm^2` to 2d.p