The partial derivatives of #z=f(x,y)=xy^2-3x^2-y^2+2x+2# are #\frac{\partial z}{\partial x}=y^2-6x+2# and #\frac{\partial z}{\partial y}=2xy-2y=2y(x-1)#.
Setting these equal to zero gives a system of equations that must be solved to find the critical points: #y^2-6x+2=0, 2y(x-1)=0#.
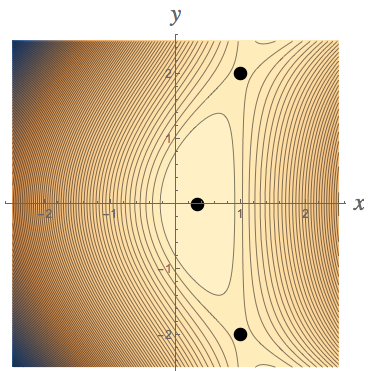
The second equation will be true if #y=0#, which will lead to the first equation becoming #-6x+2=0# so that #6x=2# and #x=1/3#, making one critical point #(x,y)=(1/3,0)#.
The second equation of the system above will also be true if #x=1#, which will lead to the first equation becoming #y^2-4=0# and #y^2=4#, making #y=\pm 2# and leading to two critical points #(x,y)=(1,2), (x,y)=(1,-2)#.
You didn't ask for this, but we can also classify these critical points as follows:
1) Find the second-order partials: #\frac{\partial^{2}z}{\partial x^{2}}=-6, \frac{\partial^{2}z}{\partial y^{2}}=2x-2#, and #\frac{\partial^{2}z}{\partial x \partial y}=\frac{\partial^{2}z}{\partial y \partial x}=2y#.
2) Find the discriminant #D=\frac{\partial^{2}z}{\partial x^{2}}*\frac{\partial^{2}z}{\partial y^{2}}-(\frac{\partial^{2}z}{\partial x \partial y})^2=12-12x-4y^2#
3) Plug the critical points into the discriminant: #D(1,2)=12-12-16=-16#, #D(1,-2)=12-12-16=-16#, and #D(1/3,0)=12-4-0=8#.
4) Since #D(1,\pm 2)=-16<0#, the critical points at #(1,\pm 2)# are saddle points.
5) Since #D(1/3,0)=8>0# and #\frac{\partial^{2}z}{\partial x^{2}}|_{(1/3,0)}=-6<0#, the critical point at #(1/3,0)# is a local maximum.
Here's a contour map of this function in the #xy#-plane along with its critical points.