Question

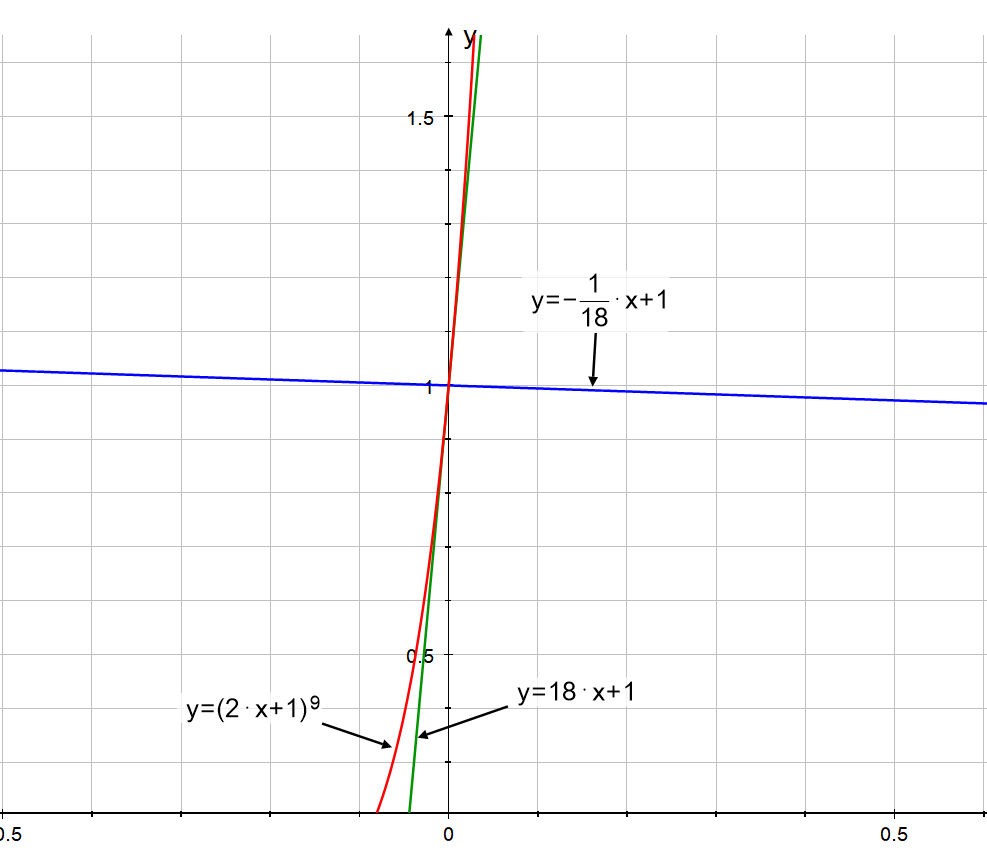
How to find the equation of the tangent and the normal of this curve?

Answer 1

Tangent line is: `color(blue)(y=18x+1)`

Normal to this is: `color(blue)(y=-1/18x+1)`

Explanation:

In order to find the equation of the tangent line, we must first find the gradient of this line at the given point.

We can do this by finding the gradient function of `f(x)=(2x+1)^9`

The gradient function is generally called the derivative:

To differentiate our function we need to use the Chain Rule.

If we let `u=(2x+1)`

Then:

`y=u^9`

This now means `y` is a function of `u` and `u` is a function of `x`

The chain rule states that:

`dy/dx=dy/(du)*(du)/dx`

I will do this step by step so you can see how it comes together.

First:

`(dy)/(du)u^9=9u^8`

But `u=(2x+1)`

So:

`(dy)/(du)(2x+1)^9=9(2x+1)^8`

Second:

`(du)/dxu=(du)/dx(2x+1)=2`

We now multiply these:

`9(2x+1)*2=18(2x+1)^8`

`:.`

`dy/dx=18(2x+1)^8`

We have the point `(0,1)`. To find the gradient at this point we plug in `x=0` into the derivative we just found:

`18(2(0)+1)^8=18`

We know `(0,1)` is a point on the line, so using point slope form of a line, where `m = "gradient"`:

`(y_2-y_1)=m(x_2-x_1)`

`1-y=18(0-x)`

`y=18x+1`

If two lines are perpendicular then the products of their gradients is `-1`

Let gradient of the normal to the line be `m`, then:

`m*18=-1`

`m=-1/18`

So we know the gradient of the normal and we also know it passes through the point `(0,1)`. Using point slope of a line again:

`y-1=-1/18(x-0)`

`y=-1/18x+1`

Tangent line is: `color(blue)(y=18x+1)`

Normal to this is: `color(blue)(y=-1/18x+1)`

GRAPH: