How to find the probability that the sample mean computed from a 25 measurements will exceed the sample mean computed from the 36 measurement by at least 3.4 but less than 5.9.?
A random sample of size 25 is taken from a normal population having a mean of 80 and a standard deviation of 5. A second sample of size 36 is taken from a different normal population having a mean of 75 and a standard deviation of 3. Find the probability that the sample mean computed from a 25 measurements will exceed the sample mean computed from the 36 measurement by at least 3.4 but less than 5.9. Assume the means to be measured to the nearest tenth.
A random sample of size 25 is taken from a normal population having a mean of 80 and a standard deviation of 5. A second sample of size 36 is taken from a different normal population having a mean of 75 and a standard deviation of 3. Find the probability that the sample mean computed from a 25 measurements will exceed the sample mean computed from the 36 measurement by at least 3.4 but less than 5.9. Assume the means to be measured to the nearest tenth.
1 Answer
Explanation:
Values we are given:
First, we must find the probability of having a difference in means between the range
This probability is equivalent to the probability of finding a z-score
and an upper bound of:
Hence, we can write:
Now we have to look up probabilities from a z-score table. We need the negative z-score table for
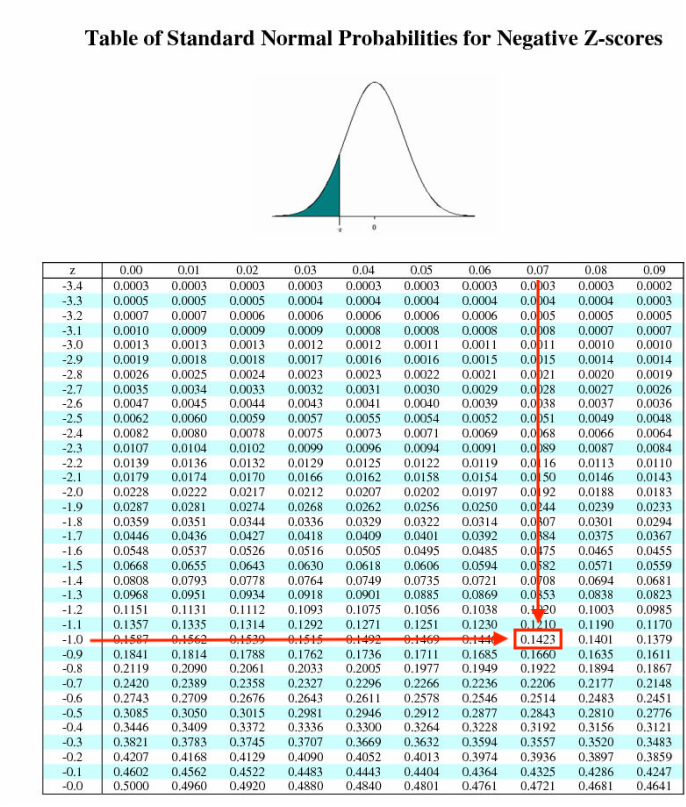
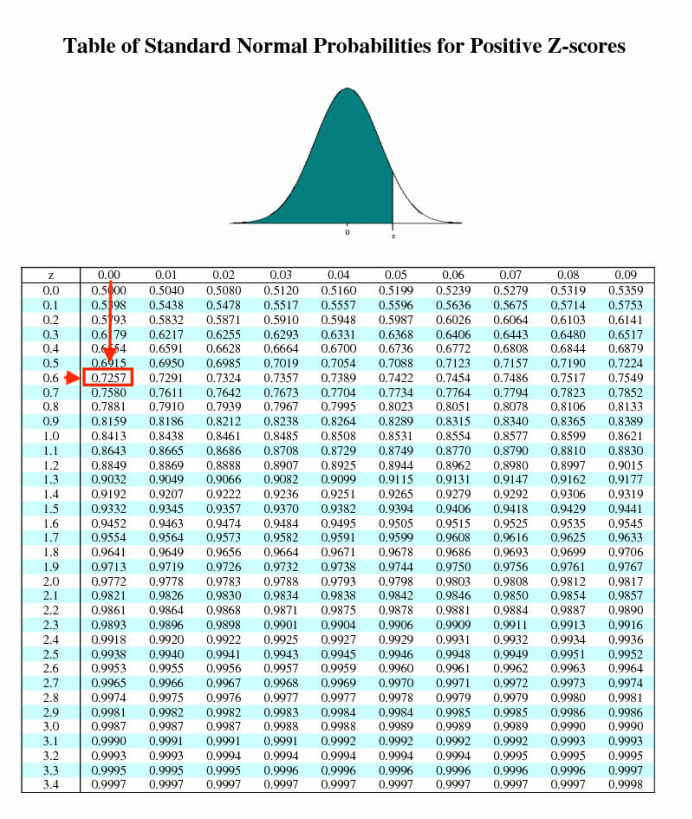
So now we have:
Hence, the probability is

