Question

a) What is the probability that the entire shipment shall be accepted? b) What is the probability that the entire shipment shall be rejected?

A shipment of 40 Mickey Mouse watches contains 6 defective ones. The shipping department selects seven of these watches and rejects the entire shipment if one or more are defective.

Answer 1

a) All 7 meet specification `->q^7 = (17/20)^7 ~~0.3206` to 4 dp

b) At least 1 fail (rejected) `1-q^7 =1-(17/20)^7~~0.6794` to 4dp

Explanation:

`color(green)("Standard notation for quality assurance gives:")`

`color(green)("Let probability of good be "q)`
`color(green)("Let probability of defective be "p " think "p->"poor quality'"`

The total ways of ordering this for a sample of 7 is: `(p+q)^7`

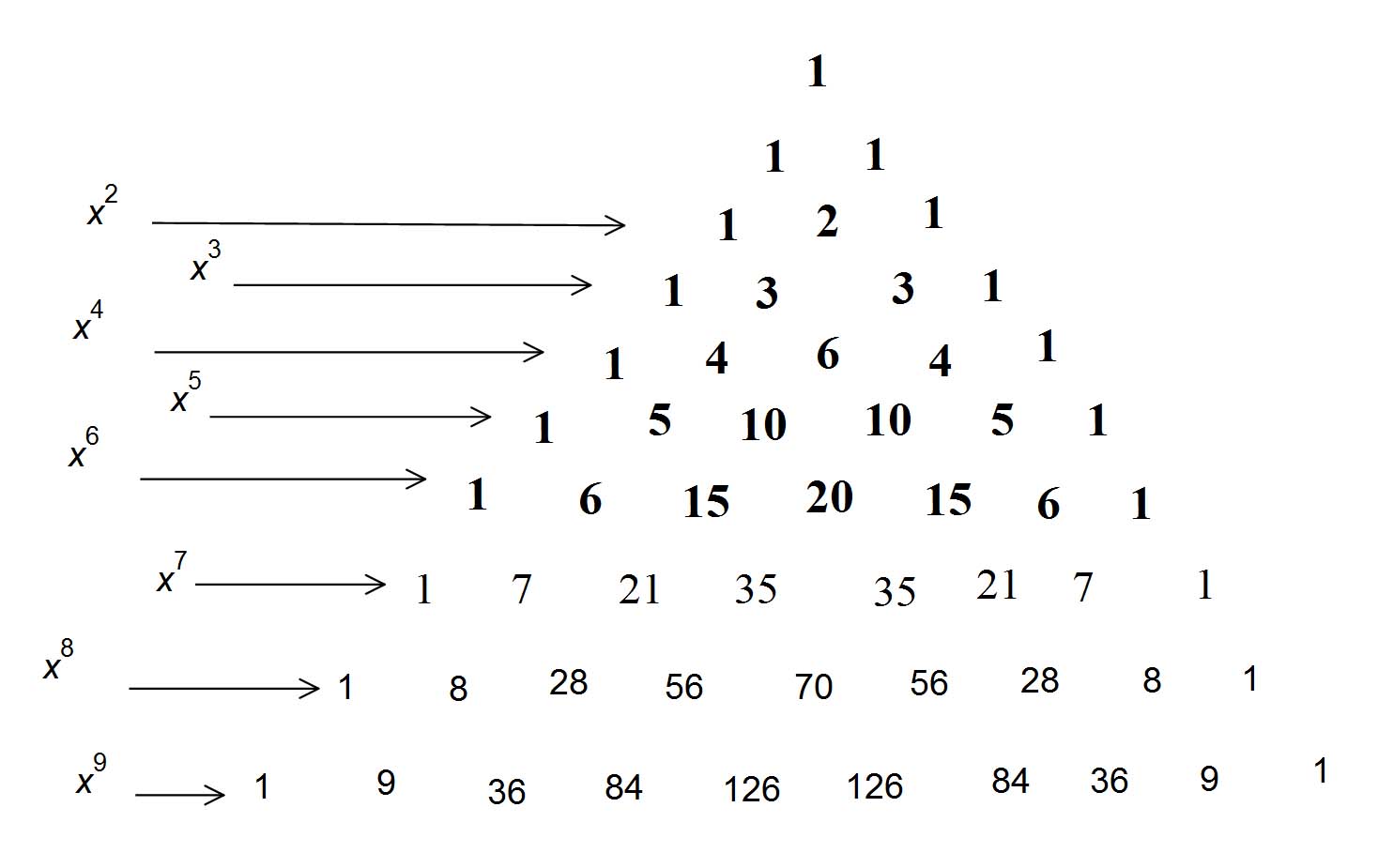
Using Pascal's triangle for Binomial expansion we select `x^7`:

`x^7" "->" "1+7+21+35+35+21+7+1`

`1p^7q^0+7p^6q^1+21p^5q^2+35p^4q^3+35p^3q^4+21p^2q^5+7p^1q^6+1p^0q^7`

`p^7+7p^6q^1+21p^5q^2+35p^4q^3+35p^3q^4+21p^2q^5+7p^1q^6+q^7`
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Accept `->` condition that has all good which is the last one of `q^7`
Reject `->` condition NOT all good which is `1-q^7`

Defective probability given as:`" "p=6/40 = 3/20`
Not defective is thus: `" "q=1-p=1-3/20=17/20`

a) All 7 meet specification `->q^7 = (17/20)^7 ~~0.3206` to 4 dp

b) At least 1 fail (rejected) `1-q^7 =1-(17/20)^7~~0.6794` to 4dp
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Comment.

It is more likely the shipment will be rejected. This is very costly for the supplier. So it would be far better for them to apply 100% inspection at the manufacture point.

The advantage of using the Binomial expansion is that it permits the probability calculation for any of the individual condition (or groups).

Suppose I wished to determine 3 poor and 4 quality. I would use the `35p^3q^4`

`=35xx(3/20)^3xx(17/20)^4`