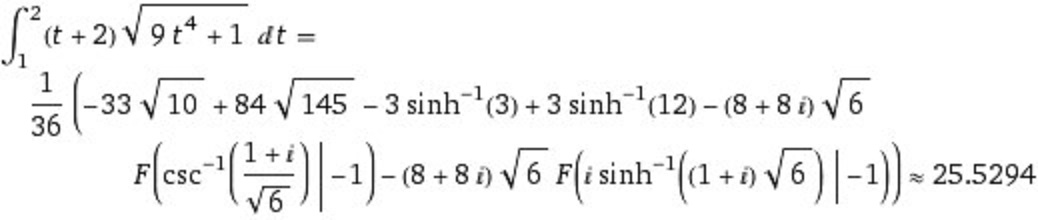How to find the surface area of revolving about axis?

#x=t^3# #y=t+2# 1<=t<=2
about y-axis

1 Answer
Sean
Mar 27, 2018

#S=160.406#

Explanation:

.

.

#x=t^3#

#y=t+2#

#1 <= t <= 2#

Let's graph the function:

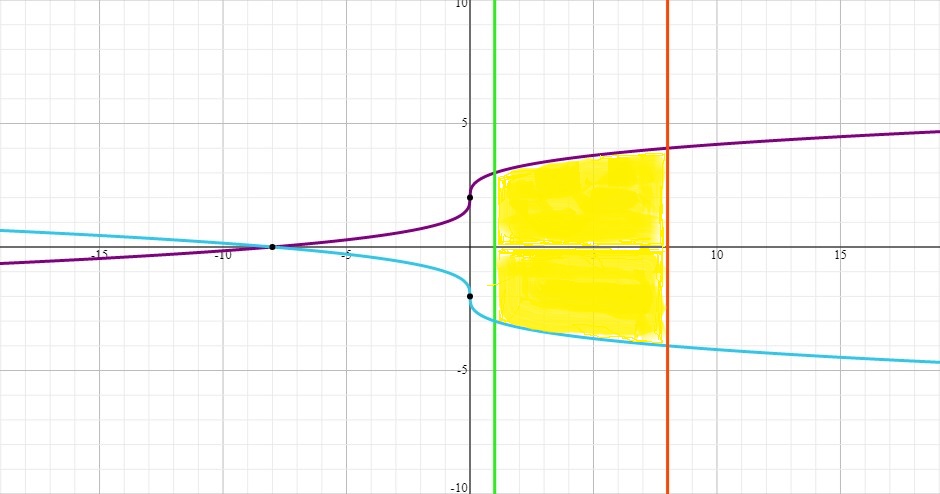
enter image source here

We need to find the surface area of the solid whose side view is shown in yellow.

The formula for the surface area #S# if the curve is revolved around the #x#-axis, and the function of the curve is given as a set of parametric equations, is:

#S=int2piy(t)ds#, and #ds=sqrt((dy/dt)^2+(dx/dt)^2)dt#

#y=t+2#

#x=t^3#

#dy/dt=1#

#dx/dt=3t^2#

#ds=sqrt(1^2+(3t^2)^2)dt=sqrt(1+9t^4)dt#

#S=int_1^2 2pi(t+2)sqrt(1+9t^4)dt#

#S=2piint_1^2(t+2)sqrt(1+9t^4)dt=2piI#

This is a difficult function to integrate. We can use an online integration tool such as Wolfram to integrate and evaluate this integral. The link to this site is:

http://www.wolframalpha.com/input/?i=int_1%5E2+((t%2B2)sqrt(9t%5E4%2B1))

The result is:

enter image source here

#S=2pi(25.5294)=160.406#

Related questions
Impact of this question
553 views around the world
You can reuse this answer
Creative Commons License