How to find the x-intercepts of this equation? #f(x)=2log_e(x+3)-5#?

Question

796 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-03-03T12:15:03

#color(blue)((e^(5/2)-3,0)#

The #bbx# intercepts occur where #bb(y=0)#

I will use #ln# to represent #log_e#

#y=2ln(x+3)-5#

#2ln(x+3)-5=0#

Add #5# and divide by #2#:

#ln(x+3)=5/2#

Raising #bbe# to the power of each side:

#e^(ln(x+3)=e^(5/2)#

By the laws of logarithms:

If #y=log_b(a)#

Then:

#b^y=a<=>b^(log_b(a))=a#

#:.#

#e^(ln(x+3)=e^(5/2)#

#x+3=e^(5/2)#

Subtract #3# from both sides:

#x=e^(5/2)-3#

#x~~9.18249396#

So #x# intercept is:

#color(blue)((e^(5/2)-3,0)#

GRAPH:

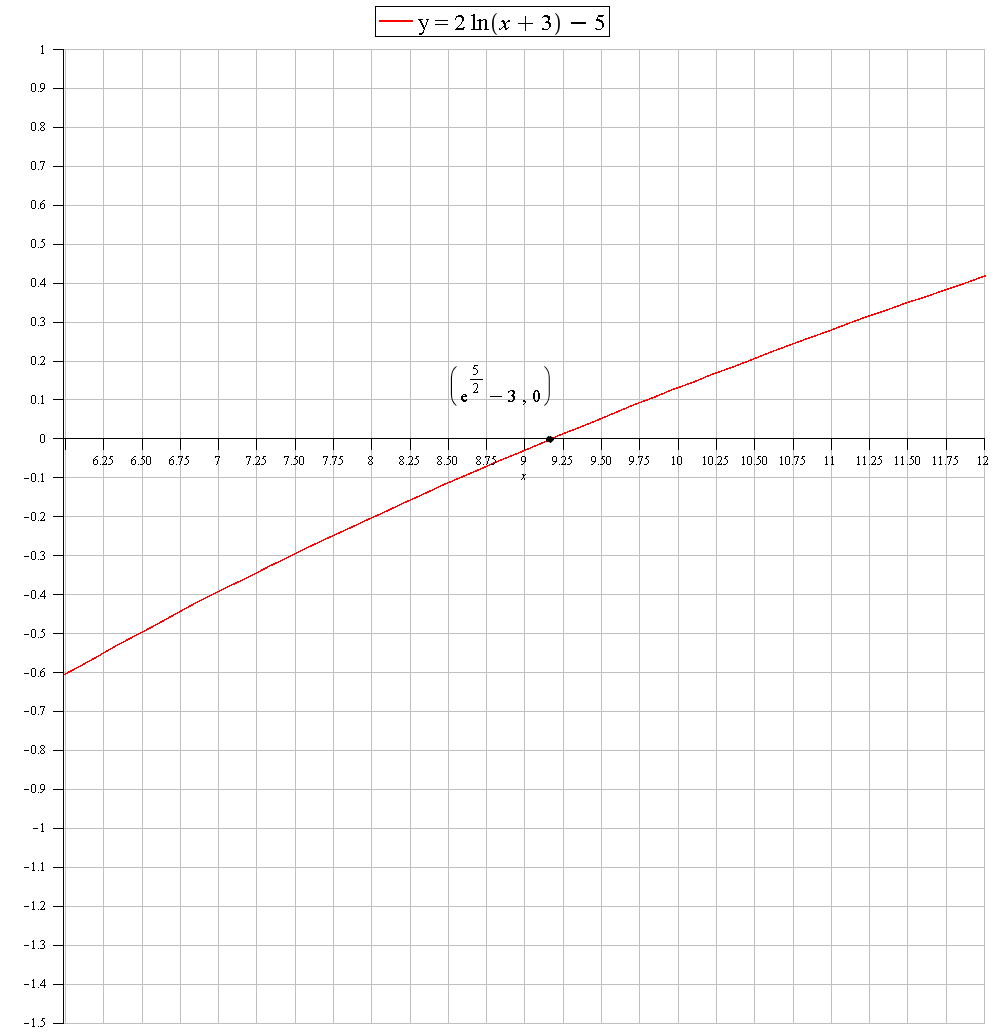
enter image source here