How to get a mathematical equation for this line of numbers: 30, 59, 91, 124 ,159, 233, 273 and 314?
I have a math problem, but I actually don't know what part of math is this.
I think it is not mathematical sequence, or any linear equation, but you get 8 numbers and you need to calculate the 9th number and write correct equation (equations) for that line of numbers.
The numbers are: 30, 59, 91, 124 ,159, 233, 273 and 314.
You may think of them as x1, x2, x3 etc.
The 9th number in "solutions" is 357.
Is it possible to get that equation for this line of numbers?
I have a math problem, but I actually don't know what part of math is this.
I think it is not mathematical sequence, or any linear equation, but you get 8 numbers and you need to calculate the 9th number and write correct equation (equations) for that line of numbers.
The numbers are: 30, 59, 91, 124 ,159, 233, 273 and 314.
You may think of them as x1, x2, x3 etc.
The 9th number in "solutions" is 357.
Is it possible to get that equation for this line of numbers?
1 Answer
It is hard to obtain the strict equation, but some approximation gives us the result
Explanation:
These numbers look like experimental data which can be approximated to a quadratic function.
Assume that the sixth term(between
I analyzed the data with Microsoft Excel and got an approximated equation:
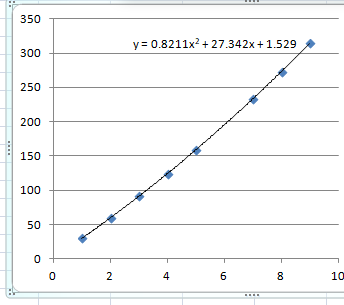
Substitute

