.
Let's look at the following figure and define parameters:
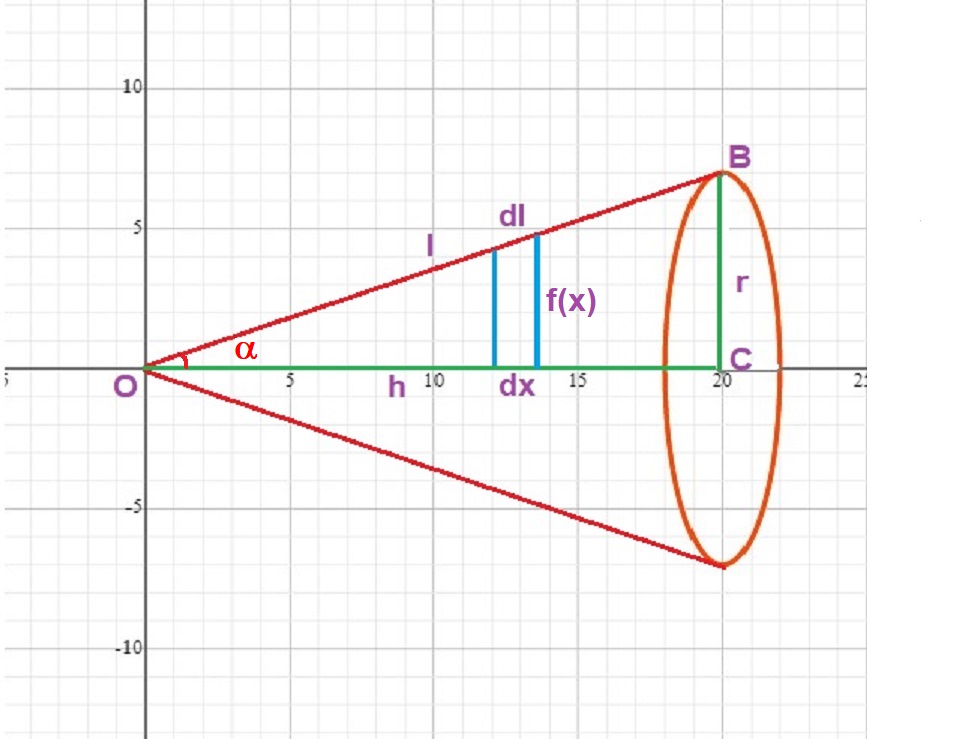
The apex of the cone is on the origin.
#OC=h# is the vertical height of the cone and lies on the #x#-axis.
#OB=l# is the lateral (slant) height of the cone.
#CB=r# is the radius of the base and is parallel to the #y#-axis.
In between the the blue vertical lines:
#dx=dh# a small increment in the vertical height of the cone.
#dl=# a small increment of the lateral height of the cone.
If we revolve line #OB# around the #x#-axis it creates the cone we see in the figure. This cone has a surface area that consists of the area of the base #+# the lateral surface area. It also has a volume.
In this case, we will only concern ourselves with the surface area. The base is a circle. Let's set up an integral to calculate the area of a circle. To do this, we will write the function of the circle in the form of #y# as a function of #x#, take its integral with respect to #x#, and evaluate it between #-r < x < r# ---- in other words, area between the curve and the #x#-axis:
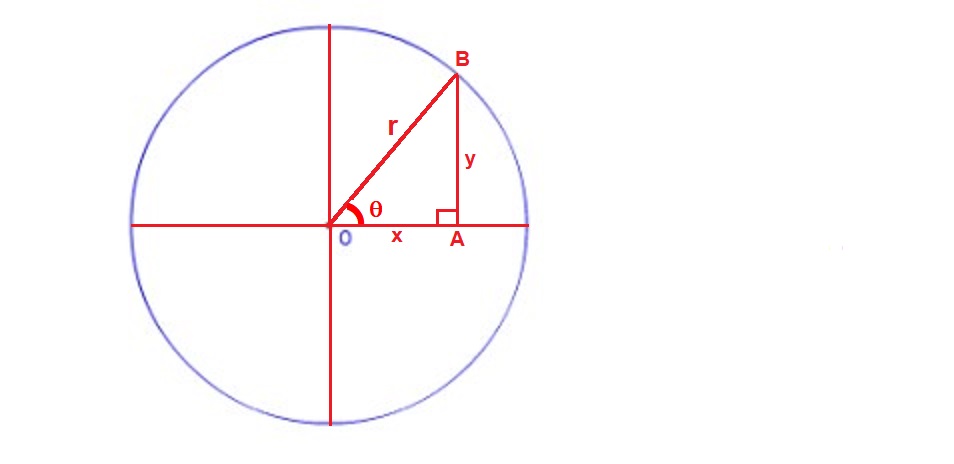
#x^2+y^2=r^2#
#y=sqrt(r^2-x^2)#
#A_("Circle")=intsqrt(r^2-x^2)dx=intsqrt(r^2(1-x^2/r^2))dx=#
#rintsqrt(1-x^2/r^2)#
If we evaluate this integral between #x=-r# and #x=r#, #(-r < x < r)#, we will get the area of half of the circle.
We will convert this integral to a trigonometric integral and compute its limits of #theta# by converting the limits of #x# above.
#x/r=costheta, :. x^2/r^2=cos^2theta=1-sin^2theta#
#theta=arccos(x/r)#
#x=-r, :. theta=arccos(-r/r)=arccos(-1)=pi#
#x=r, :. theta=arccos(r/r)=arccos(1)=0#
Therefore,
#-r < x < r# becomes #pi < theta< 0#
#dx/r=-sinthetad theta#
#dx=-rsinthetad theta#
#1/2A_("Circle")=rint_pi^0sqrt(1-1+sin^2theta)(-rsinthetad theta)=-r^2int_pi^0sin^2thetad theta=-r^2int_pi^0(1-cos(2theta))/2d theta=-r^2int_pi^0(1/2)d theta+r^2int_pi^0(1/2)cos(2theta)d theta=(-r^2/2theta+r^2/2(1/2sin(2theta)))_pi^0=(r^2/4(sin(2theta)-2theta))_pi^0#
#1/2A_("Circle")=r^2/4((sin(2theta)-2theta))_pi^0=r^2/4(sin(2(0))-2(0)-sin(2pi)+2pi)=r^2/4(0-0-0+2pi)=(2pir^2)/4=(pir^2)/2#
Therefore,
#color(red)(A_("Circle")=2((pir^2)/2)=pir^2)#
To find the lateral surface area of the cone, which results from revolving #OB# around the #x#-axis, is accomplished by calculating the surface area of a small slice of the cone with thickness of #dx#, as shown on the figure by the blue vertical lines. Adding the surface areas of these slices together would give us the lateral surface area.
When #dx# is infinitely small, the thickness becomes #0# and the surface area of the slice reduces to the circumference of a circle. Adding an infinite number of these circumferences together results in the lateral surface area of the cone.
We accomplish this by using the function of a circle, and using an integral to calculate its arc length, and evaluating it between #0# and #h#.
This will give us the circumference of half of the circle. We then multiply it by #2# to get the full circumference.
The function of a circle, as noted above, is:
#x^2+y^2=r^2 ory=sqrt(r^2-x^2)#
#2xdx+2ydy=2rdr#
Since #r# is constant, #dr=0#
#2xdx+2ydy=0#
#2ydy=-2xdx#
#ydy=-xdx#
#dy/dx=-x/y#
#dy/dx=-x/sqrt(r^2-x^2)#
The arc length #L# is:
#L=intds# where #ds=sqrt(1+(dy/dx)^2)dx#
Half the circumference of the circle is:
#L=int_(-r)^rsqrt(1+(-x/sqrt(r^2-x^2))^2)dx=int_(-r)^rsqrt(1+x^2/(r^2-x^2))dx=int_(-r)^rsqrt((r^2-x^2+x^2)/(r^2-x^2))dx=int_(-r)^rsqrt(r^2/(r^2-x^2))dx#
#x=rcostheta#
#dx=-rsinthetad theta#
#L=int_pi^0sqrt(r^2/(r^2-r^2cos^2theta))(-rsinthetad theta)#
#L=int_pi^0sqrt(r^2/(r^2(1-cos^2theta)))(-rsinthetad theta)#
#L=-rint_pi^0sqrt(1/sin^2theta)sinthetad theta#
#L=-rint_pi^0(1/sintheta)sinthetad theta=-rint_pi^0d theta=-rtheta)_pi^0#
#L=-r(0-pi)=pir#
Full circumference of the circle is:
#color(red)(2L=2pir)#
Now, we will use this circumference in the integral for the lateral surface area of the cone:
#S=int_0^h2pif(x)dl#
But the radius of the circle, as shown in the first figure above, is:
#y=f(x)#
#cosalpha=h/l#
#l=h/cosalpha#
#dl=(dh)/cosalpha=dx/cosalpha#
#tanalpha=f(x)/x=r/h#
#f(x)=xtanalpha#
#S=int_0^h2pixtanalphadx/cosalpha#
#tanalpha#and #cosalpha# are constants since the angle #alpha# is constant:
#S=2pitanalpha/cosalphaint_0^hxdx#
#S=2pi(r/h)/(h/l)1/2x^2)_0^h=2pi(rl)/h^2*1/2h^2=cancelcolor(red)(2)pi(rl)/cancelcolor(red)(h^2)*1/cancelcolor(red)(2)cancelcolor(red)(h^2)#
Therefore, the lateral surface area of a cone is:
#color(red)(S=pirl)#
The total surface area of a cone is:
#color(red)(S_("Cone")=pir^2+pirl)#



