Question

How to I find the degrees of a line given it's slope?

For example, a flagpole is tilted back and has a slope of -5 (with the ground being the x-axis). What is it's angle to the ground in degrees?

Answer 1

For a straight line when expressed in the slope-intercept form as

`y=mx+c`

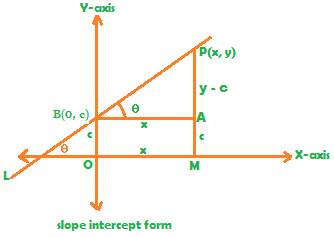
we know that `m` is the slope of the line which it makes with `x`-axis and `c` is intercept on the `y`-axis.

Also that by definition `m-=tan theta`,
where `theta` is the angle line makes with the `x`-axis.

`:. theta=tan^-1m`

For the given problem `m=-5`
This implies that the angle `theta` is more than `90^@` and lies in the second quadrant as shown below.

`theta=tan^-1(-5)`
Now using tables or a calculator we get
`theta=-78.7^@`, rounded to one decimal place.
This angle is as measured from `-x` axis in the opposite direction as indictaed by `-ve` sign.

Or Angle of the flagpole`=180-78.7=101.3^@` as measured normally.