How to prove that ACD is an equilateral triangle?
DB is the diameter in a circle with the center S, . The line AC goes 90 degrees from the center point M of the line SB. "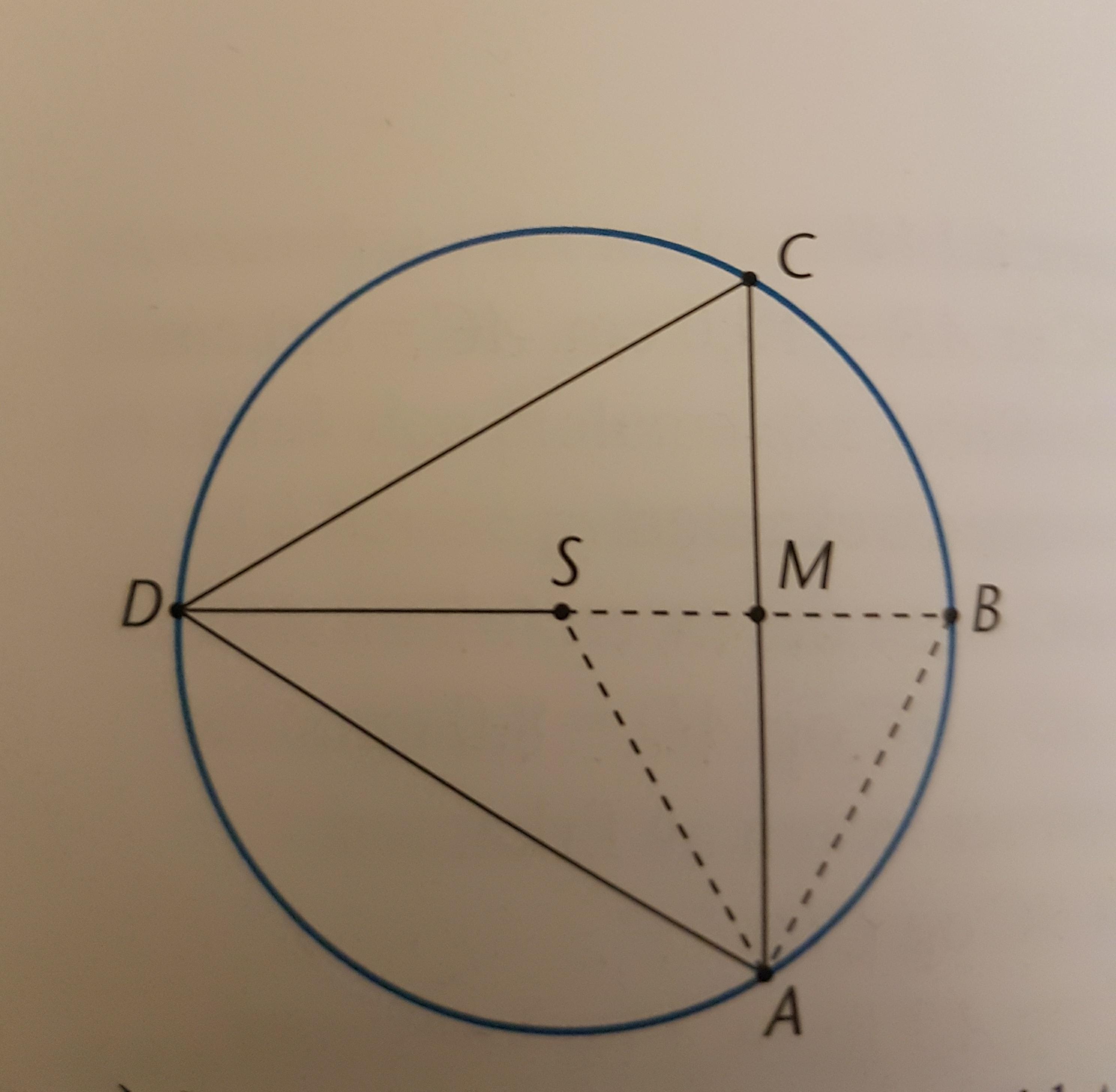
DB is the diameter in a circle with the center S, . The line AC goes 90 degrees from the center point M of the line SB. "
3 Answers
Hence
Explanation:
Let r be the radius of the circle.
Triangles SAM & BAM are congruent as
SM = BM = r / 2, AM common & /(SMA) = /(BMA) = 90^0#
#:. Delta SAB is equilateral.
In triangle ADC, DM bisects AC at right angle.
Since sides AD, DC & AC are equal and
see explanation
Explanation:
The given conditions are shown in the figure.
Let
similarly,
As
Hence,
DB is the diameter in a circle with the center S, . The line AC goes 90 degrees from the center point M of the line SB. "
Given that the line AC goes 90 degrees from the center point M of the line SB.
So in
Hence
So
Again
So
Now being diameter the semicircular
So in
Now diameter
So DB bisects AC at M.
This means
Hence
So
So

