Question

How to sketch this sin graph?

Answer 1

See below.

Explanation:

We can express this function in the form:

`y=asin(bx+c)+d`

Where:

• `color(white)(888)bba` is the amplitude.

• `color(white)(88)bb((2pi)/b)` is the period. ( this is the normal period divided by `bb(b))`

• `color(white)(88)bb((-c)/b)` is the phase shift.

• `color(white)(888)bbd` is the vertical shift.

`y=2sin2(x+pi/6)+1`

Multiply the bracket by the `2`:

`y=2sin(2x+pi/3)+1`

We can see from this, that:

Amplitude is `bb2`

Period is `(2pi)/2=bbpi`

Phase shift is `(-pi/3)/2=-pi/6`

Vertical shift is `1`

If we look at this in relation to `y=sin(x)`, we see that.

The amplitude has been increased by a factor of `bb2`. this causes the graph of `bb(y=sin(x))` to be expanded by a factor of `bb2` in both the positive and negative `bby` direction.

I'll plot all the different changes in relation to `bb(y=sin(x))`

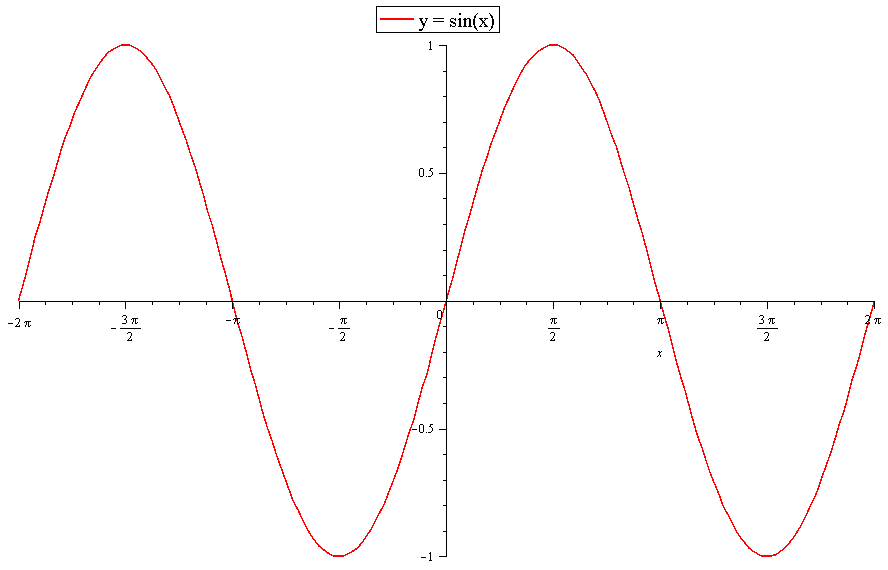
This is shown in the graph `bb(y=2sin(x))`

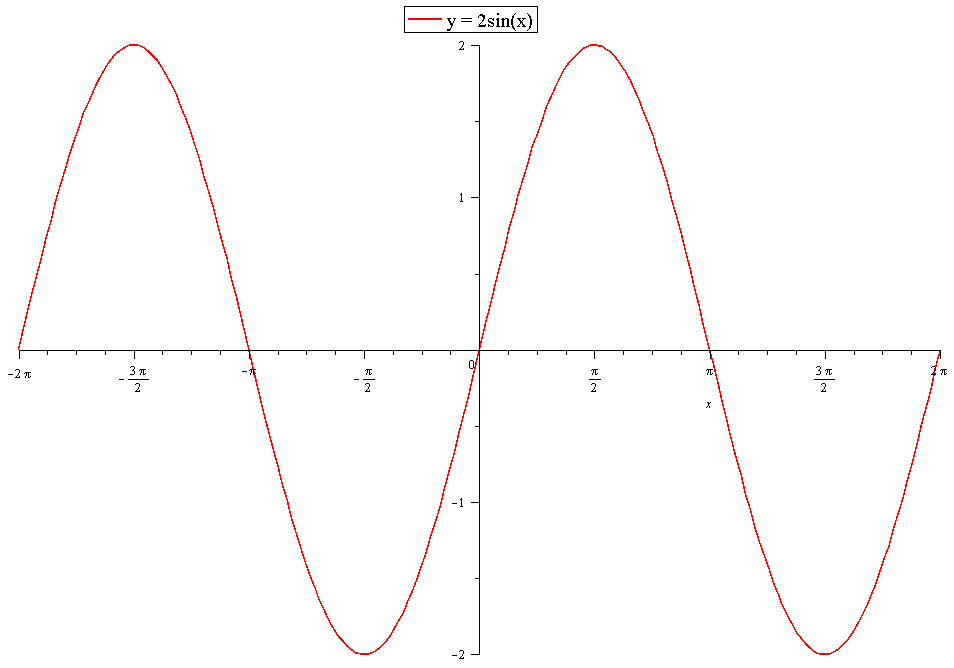
The period has been compressed by a factor of `bbpi` in the horizontal direction.

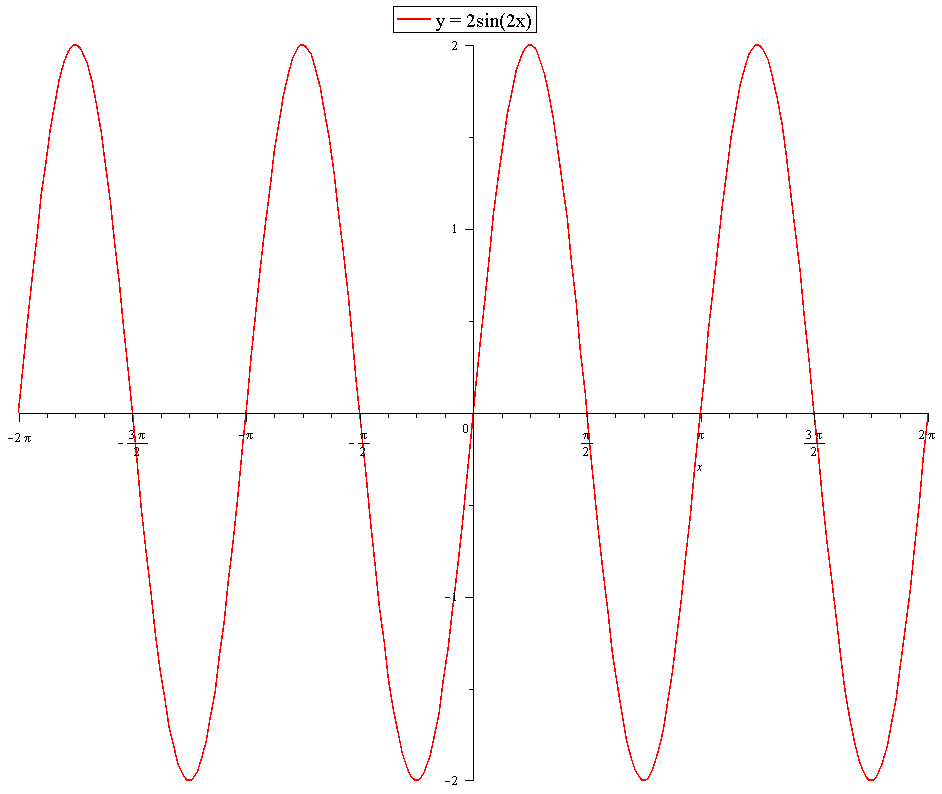
The phase shift is `bb(-pi/6)`, this causes the graph of `bb(y=sin(x))` to be translated `bb-pi/6` units in the negative `bbx` direction.

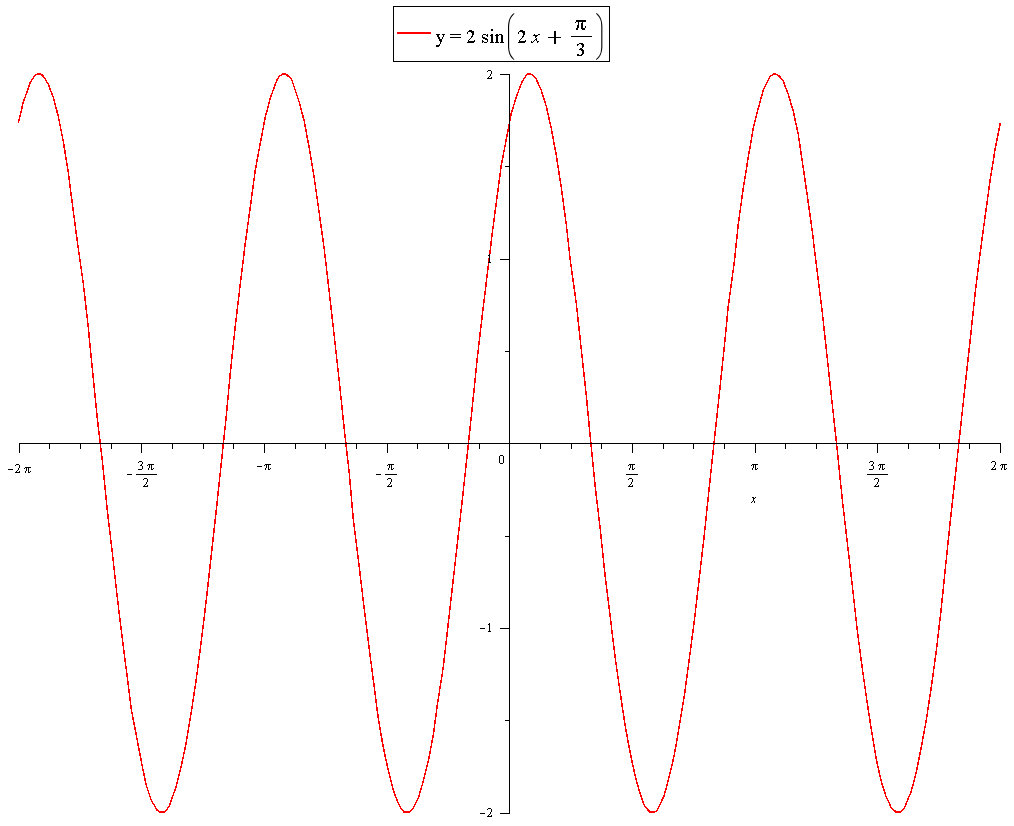
The vertical shift is `bb1`, this causes the graph of `bb(y=sin(x))` to be translated `bb1` unit in the positive `bby` direction.

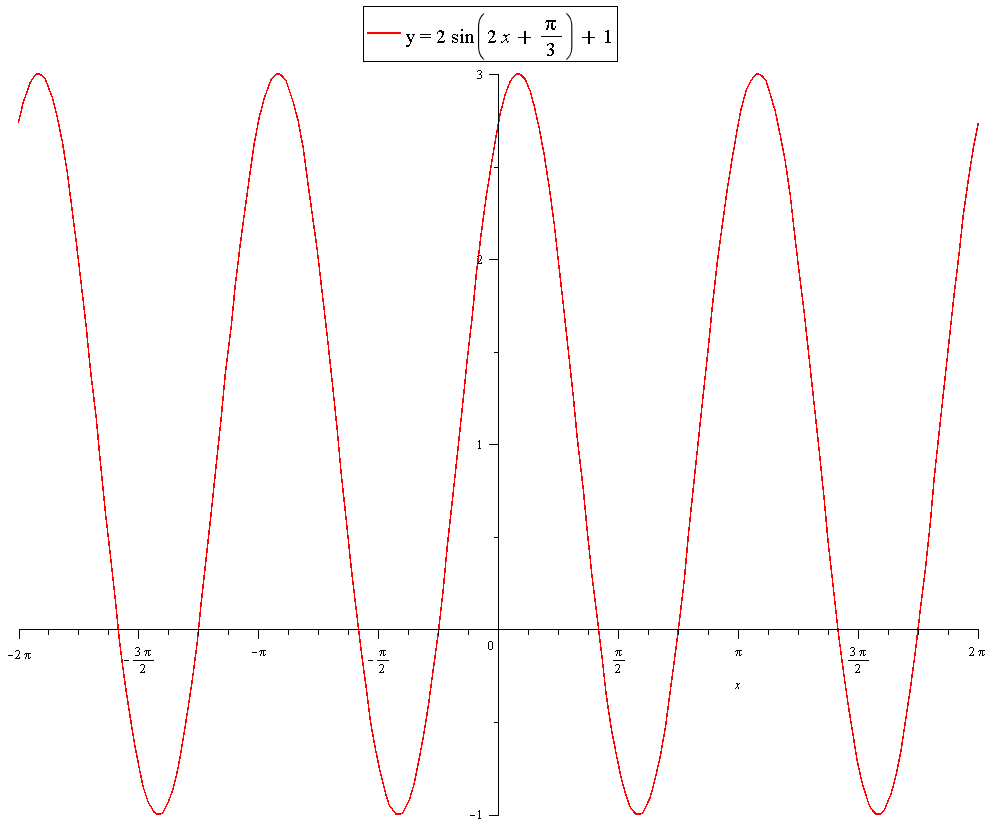
This is now complete.

Here is a link that explains all the different parts of trig function graphs. It would be worth taking a look. It includes lots of graphics so you can see exactly what's happening.

https://www.mathsisfun.com/algebra/amplitude-period-frequency-phase-shift.html.